Exercícios de Método de Newton-Raphson - Lista de Exercícios Resolvida
Questão 1
Seja .
Verifique que possui um zero no intervalo ;
Justifique teoricamente o comportamento da sequência colocada a seguir, gerada pelo método de Newton para o cálculo do zero de em , com e precisão .
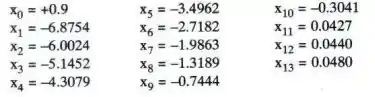
Questão 2
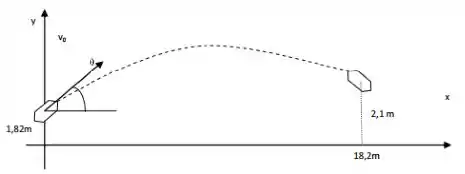
Um jogador de futebol americano está prestes a fazer um lançamento para outro jogador de seu time. O lançador tem uma altura de e o outro jogador está afastado. A expressão que descreve o movimento da bola é a familiar equação da física que descreve o movimento do projétil:
Onde e são as distâncias horizontal e vertical, respectivamente, é a aceleração da gravidade. é a velocidade inicial da bola quando deixa a mão do lançador e é o ângulo que a bola faz com o eixo horizontal nesse mesmo instante. Para , , e , determine o ângulo no qual o jogador deve lançar a bola.
Resolva o problema com tolerância rad.
Ver solução completaQuestão 3
Dê um exemplo de função , que tenha pelo menos uma raiz, onde o Método de Newton-Raphson não converge sempre.
Ver solução completaQuestão 4
Encontre as duas raízes reais do polinômio abaixo pelo método de Newton-Raphson com precisão .
Ver solução completaQuestão 6
Uma pessoa tomou um empréstimo de reais, que acrescenta os juros no total antes de computar o pagamento mensal. Assim, se a taxa mensal de juros, em porcentagem, é e o empréstimo é pelo prazo de meses, a quantia total que o tomador concorda em pagar é:
Isto é dividido por para dar o total de cada pagamento , ou seja,
Isto é perfeitamente legal e muito usado em lojas de departamento. (É chamado o empréstimo com acréscimo). Mas a verdadeira taxa de juros que o tomador está pagando é alguma coisa além de , porque ele não conserva o total do empréstimo por todos os meses: Ele está pagando-o de volta com o decorrer do tempo. A verdadeira taxa de juros pode ser encontrada pela determinação de uma raiz da equação:
Isto fornece a taxa de juros por período de pagamento, que pode ser convertida em taxa anual multiplicando-se a mesma por 12. Seja , e . Determine a verdadeira taxa de juros com precisão de .
Ver solução completaQuestão 7
Use o Método de Newton para encontrar soluções com precisão de para os seguintes problemas:
para
para e
para e
para e
Ver solução completaQuestão 8
Seja e . Use o Método de Newton para encontrar . O valor poderia ser usado?
Ver solução completaQuestão 9
Encontre um valor aproximado para no intervalo com precisão de , para a equação populacional:
Ver solução completaQuestão 10
O valor de pode ser obtido através da resolução das seguintes equações: e . Aplique o Método de Newton-Raphson com e precisão em cada caso e compare os resultados. Explique a diferença no número de iterações realizadas para atingir a precisão.
Ver solução completaQuestão 11
3. Dada a função :
a) Aplique o método de Newton para encontrar um valor aproximado da raiz de . Para cada iteração, apresente os valores de e . Considere, utilize 4 casas decimais e arredondamento padrão. Utilize como critério de parada 3 iterações () ou .
b) Complemente a implementação do código abaixo para encontrar o zero da função pelo método da Falsa Corda utilizando 50 iterações como critério de parada. Considere o intervalo de separação . OBS: Em C, a equação pode ser escrita como.

Questão 12
4. Seja a o número de letras do seu primeiro nome, e sejam e .
(a) construa um polinômio de grau que tenha exatamente como raízes os números , e ;
(b) escolha entre , e e mostre (através de cálculos) que o número escolhido trata-se, de fato, de uma raiz do polinômio;
(c) escreva a fórmula de iteração do método de Newton para encontrar raízes desse polinômio;
(d) escolha uma aproximação inicial e realize uma iteração do método de Newton para encontrar uma aproximação para a raiz escolhida. Apresente todo o desenvolvimento da questão.
Ver solução completaQuestão 13
4) Determine e tal que qualquer que seja o polinômio de grau menor ou igual a 3. Seja e use a expressão para estimar e delimite o erro cometido, de acordo com a estimativa de erro. Use o valor exato de apenas para confirmar sua delimitação de erro.
Ver solução completaQuestão 14
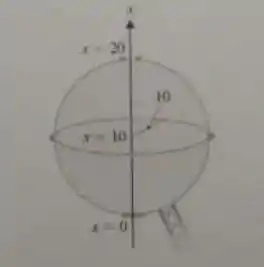
3) Suponha um tanque de água esférico com raio 10 dm conforme a figure abaixo. Determine o nível de água (com erro menor que 1mm) tal que o tanque fique preenchido com 1/3 do seu volume, utilizando para tal o método de Newton. Justifique a convergência do método de Newton.
Questão 15
2)
a) Mostre que a função tem um único ponto de mínimo positivo.
b) Calcule uma aproximação para este ponto utilizando o método de Newton (calcule 3 iterações a partir de . Mostre que o método de Newton é convergente para esta escolha de )
c) Sem determinar o valor da solução verifique se o valor determinado no item b dista menos que do ponto de mínimo. Justifique.
Ver solução completaQuestão 16
2)
a) Mostre que a função tem um único ponto de mínimo positivo.
b) Calcule uma aproximação para este ponto utilizando o método de Newton (calcule 3 iterações a partir de . Mostre que o método de Newton é convergente para esta escolha de )
Ver solução completaQuestão 17
3. Dada a função :
a) Aplique o método de Newton para encontrar um valor aproximado da raiz de f(x). Para cada iteração, apresente os valores de e . Considere = e utilize 4 casas decimais e arredondamento padrão. Utilize como critério de parada 4 iterações (i = 0, 1, 2, 3, 4) ou |f(xi)|
b) Complemente a implementação do código a seguir para encontrar o zero da função f(x) pelo método da Bissecção utilizando |f(xi)|
