Teste da Comparação
Produzido por Carolina SabaTeoria
Fala aí galera bonita. Sejam muito bem-vindos ao Responde Aí, a plataforma de exatas criada para levar até você um ensino sensacional, didático e descontraído para você arrasar nas provas!
Nossa missão aqui hoje é entender o teste da comparação, partiu?
Conhecimentos Prévios
Teste da Comparação
Uma das coisas que mais queremos saber sobre as séries é se elas convergem ou divergem e, para isso existem diversos testes que podemos fazer para chegar a uma conclusão, entre esses testes está o teste da comparação.
O teste da comparação, como o próprio nome já diz, basea-se na comparação de uma série com outra.
Vamos entender como aplicar esse teste com um exemplo, beleza?
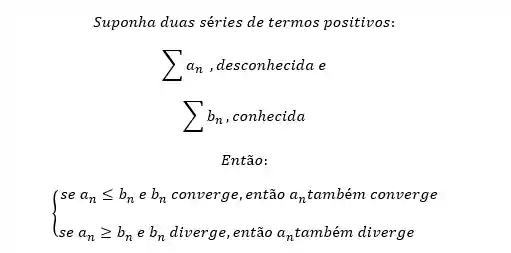
Dá uma olhada nessa série aqui:
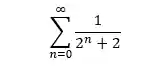
Vamos usar essa série de exemplo e fazer um passo a passo de como aplicar o teste da comparação.
PASSO 1: A primeira coisa que vamos fazer para aplicar o teste da comparação é encontrar uma série que tenha o termo geral parecido com a série que queremos analisar. Se a gente reparar bem, essa nossa série exemplo tem certa semelhança com a série geométrica.
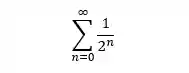
Essa série que encontramos com o termo geral parecido será chamada de série de teste.
PASSO 2: Agora, o que temos que fazer é ver se a nossa série teste é convergente ou divergente.
Para o nosso exemplo, a série teste converge, pois é uma série geométrica com
PASSO 3: Nosso terceiro passo é encontrar uma relação entre o termo geral da série teste e o termo geral da série que queremos analisar.
Se olharmos bem vemos que o termo geral da série que queremos analisar é sempre menor que o termo da série teste, pois há um
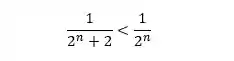
PASSO 4: Após encontrar uma relação para os termos gerais, essa relação é estendida para a série toda.
Em outras palavras, se o termo geral da série que estamos analisando é menor que o da série de teste, então a série toda que estamos analisando é menor que a série de teste.
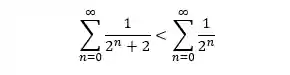
PASSO 5: Uma vez achada a relação entre as séries vamos aplicar de fato o teste da comparação.
O teste da comparação em geral diz o seguinte:
Confuso? Vou te explicar melhor.
O teste fala assim: se a série que a gente quer conhecer for menor do que outra série que sabemos que é convergente, então a série desconhecida é convergente. É exatamente esse caso que encontramos ali em cima no nossa exemplo, vimos que a série teste é convergente e que a série que desconhecemos e queremos analisar é menor que a teste, então a desconhecida converge.
O outro caso que o teste diz é: se a série desconhecida for maior do que uma série que sabemos que diverge, então a desconhecida também divergirá!
Tranquilo, não é?
Mas vamos ver agora uma coisa que precisamos ficar bem atentos.
Erro ao se aplicar o teste da comparação
Agora cuidado! O teste não afirma nada a respeito de séries maiores do que séries que convergem ou menores do que séries que divergem, nesses casos não podemos afirmar nada sobre a convergência e aí temos que procurar outro método.
Se liga nessa série aqui:
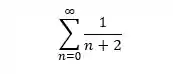
Ela se parece muito com essa série teste aqui, que é divergente:
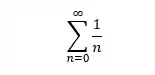
Quando relacionamos os termos gerais temos o seguinte:
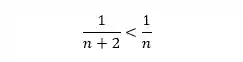
A nossa série desconhecida é menor do que uma série que diverge e o teste da comparação não fala nada sobre isso, ele fala sobre a série desconhecida ser maior que uma conhecida que diverge. Então nesse caso não podemos afirmar nada e o teste da comparação não é tão útil aqui.
E esse é o teste da comparação.
Além de termos esse conteúdo em texto nós temos ele em vídeo também. Então, se você prefere assistir uma boa aula não deixa de conferir o vídeo que eu vou deixar aqui embaixo 👇🏽
Vídeo
Como falamos lá no início o teste da comparação é apenas um dos testes que podemos fazer para saber se uma série converge ou diverge. Você pode conhecer os outros teste aqui mesmo no Responde Aí, só conferir essas páginas aqui: Teste da Divergência e Teste da comparação no limite.
Curtiu nosso conteúdo? Então assina com a gente para ter acesso a muito mais!
Exercícios Resolvidos
Exercício Resolvido #1
James Stewart, Cálculo Vol. 2, tradução da 6ª ed. Norte-americana, Rio de Janeiro: CENGAGE learning, 2010, pp. 672, exercício 3
Determine se a série converge ou diverge
Passo 1
Pelo formato da série, já vemos que o termo geral tende a zero quando tende a infinito, logo, o Teste da Divergência não será útil aqui.
Vamos, então, tentar o Teste da comparação e, para isso, precisamos de um palpite sobre a convergência dessa série. Como o denominador cresce muito rápido, parece que o termo geral tende a zero rapidamente, o que nos leva a pensar que a série converge.
Passo 2
Certo, então precisamos encontrar uma série de termos maiores que a do problema que convirja. Podemos usar a p - série de :
Essa série é convergente!
Passo 3
Como
Sabemos que
Então confirmamos que a série escolhida é maior que a do problema! E prontinho! Pelo Teste da Comparação, a série do problema converge já que também converge! Feshow.
Resposta
A série converge.
Exercício Resolvido #2
James Stewart, Cálculo Vol. 2, tradução da 6ª ed. Norte-americana, Rio de Janeiro: CENGAGE learning, 2010, pp. 669, exemplo 2
Teste a série
Quanto a convergência ou divergência.
Passo 1
Como o termo geral da série tende para zero, o Teste da divergência não nos ajuda aqui, vamos tentar usar o da comparação. Antes, precisamos ter uma ideia sobre a convergência.
Essa série se parece bastante com a harmônica
Então, parece que essa série tende a divergir também. É isso que tentaremos provar!
Passo 2
Precisamos, então, mostrar que a série do problema tem termos maiores dos que os de uma série que diverge. Aqui, temos um detalhe interessante, perceba que podemos dizer o seguinte:
Mas para todos os valores? Não, apenas quando
Ou seja,
Como o valor de é não inteiro e maior que , podemos afirmar que a relação acima vale para . Mas podemos fazer esse tipo de restrição para aplicar o Teste da comparação? Sim, pois o que importa para o teste é a tendência das séries do infinito, pois é assim que analisamos a convergência.
Então, como a partir de , a série do problema tem termos maiores que os da Série harmônica, pelo Teste da comparação, podemos dizer que ela diverge.
Resposta
A série diverge.
Exercício Resolvido #3
James Stewart, Cálculo Vol. 2, tradução da 6ª ed. Norte-americana, Rio de Janeiro: CENGAGE learning, 2010, pp. 672, exercício 7
Determine se a série converge ou diverge.
Passo 1
Como o termo geral da série tende para zero, sabemos que o Teste da divergência não é útil aqui. Já que a expressão de é relativamente simples, parece uma boa tentar aplicar o Teste da comparação.
Antes de tudo, precisamos ter uma ideia sobre a convergência da série, para saber com o que comparar.
Essa série se parece com uma série geométrica de , não é? O termo geral parece que tende rápido para zero, como na geométrica, então, imaginamos que essa série convirja.
Passo 2
Vamos, então, comparar essa série com a geométrica que acabamos de mencionar
Como temos , sabemos que essa série converge. Certo, agora vamos comparar as duas séries. Sabemos que
Portanto, podemos dizer que
Como os termos da série do problema são menores que os de uma série que converge, pelo Teste da comparação, sabemos que essa série converge.
Resposta
A série converge.
Exercício Resolvido #4
PUC-RJ - Cálculo 3 - P3 2014.1 - 1d
Diga se a série abaixo converge ou diverge.
Passo 1
A ideia aqui é utilizar o teste da comparação pra dizer se a série converge ou diverge.
Só que tem um detalhe, a nossa série tem termos negativos e esse teste só é válido para séries de termos positivos. O que a gente faz nesse caso?
Vou te passar uma dica muito boa:
Se for convergente, então também é convergente.
Então, se eu puder verificar que o módulo dessa série converge, então a série vai convergir.
Repare que podemos dizer que:
Como e é sempre positivo, seja qual for o valor de , podemos afirmar que:
Visto que e .
E repare que também podemos dizer que:
Então, pelo teste da comparação, temos:
Passo 2
Então, concluímos que, como:
E converge, a série converge absolutamente!! Então a série converge!
Resposta
A série converge.
Exercício Resolvido #5
UFRJ - Cálculo 4 - P1 2012.1 - 2b
Estude a natureza das séries abaixo:
Passo 1
Oi, galerinha, antes de começar a estudar essa série, eu proponho uma coisinha! É um pouco complicado aplicar o Teste da comparação quando temos muitos termos no numerador, então minha proposta é dar uma mexida na cara dessa função.
Lembra daquele produto notável ? Usando essa ideia, se a gente multiplicar o numerador por conseguimos nos livrar da raiz. Fica assim, olha:
Certo, conseguimos nos livrar das raízes no numerador, mas e agora?
Passo 2
Agora vamos escolher uma série parecida que a gente saiba a convergência para descobrir se a nossa série converge ou diverge.
Eu acho mais simples pensar sem as raízes nos denominador. Deste modo, seria muito interessante se tivéssemos no denominador, pois as raízes iriam sumir. Repara,
Quando fizemos isso, chegamos a uma série que diverge. Se você ta se perguntando o por quê que ela diverge, dá uma olhada nesse truque, considerando , temos:
Ou seja, a série diverge porque ela nada mais é do que a série harmônica, só que começando em ! E a harmônica galera, diverge.
Ok, mas em que isso nos ajuda? Olha o seguinte:
Ou seja, mostramos, por meio de muitas bruxarias, que a série do problema tem termos maiores que os de uma série que diverge, logo, ela também diverge.
Resposta
A série diverge.