21) Seja um campo vetorial de classe , em tal que , para todo . Sabendo que , onde , calcule
Onde .
Passo 1
Bem, eu sei que está muuuito confuso o enunciado e que apareceram várias informações, porém o que o problema quer na realidade é uma integral de linha:
Onde a curva é uma curva fechada dentro dessa elipse e de equação :
Pow! Então eu te recomendo que você não se preocupe agora com aquelas outras informações dadas agora e que comece a resolvendo a integral de linha normalmente como estamos acostumados:
- Como estamos em uma região fechada, aplicando o nosso amigo “O Teorema de Green” ! Venha comigo! :D
Passo 2
O teorema de Green nada mais é do que essa igualdade mara entre a integral de linha com uma integral dupla:
Mas antes de aplicarmos essa igualdade maravilhosa do Teorema, temos que avalizar as condições de Green, que sempre nos exige:
1º - Uma região fechada pela borda .
2º - Orientadas positivamente.
3º - Um campo sem singularidades onde estamos trabalhando.
Vamos averiguar?
Passo 3
Sobre uma curva fechada está ok, pois a como já vimos, a curva que queremos a integral de linha
Ela é fechada, inclusive foi a nossa inspiração inicial para aplicar o Teorema, certo? E delimita o interior da elipse:
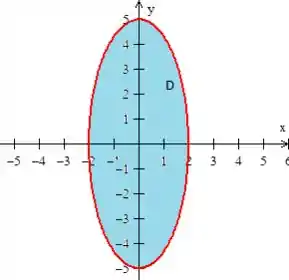
E em relação a ser orientada positivamente também está ok, pois quando um problema não nos diz nada sobre a orientação, adotamos a curva girando no sentido anti-horário... Orientada positivamente, portanto. :D
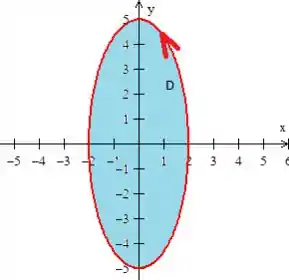
Passo 4
Quanto à terceira exigência... Campo sem singularidades não está sendo satisfeito, pois o campo é de classe dentro do . No ponto , ele tem uma singularidade, ou melhor, um problema de definição saca?
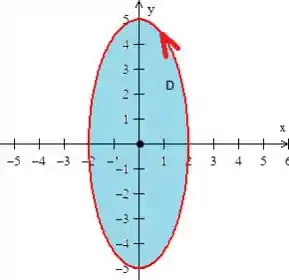
Por isso o que vamos fazer é “empacotar “ esse ponto com uma outra curva... A circunferência e de raio do enunciado:
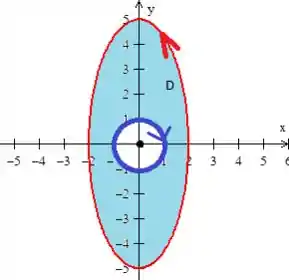
Então a nossa região sofre um recorte.
O bordo dela agora é a curva e a curva (a circunferência azul)e note também que tem que necessariamente estar girando no sentido horário para o conjunto estar orientado positivamente.
Passo 5
Condições do Teorema sendo satisfeitas, podemos aplicar a igualdade numa boa:
Bem, cuidado que aqui tem um detalhe muito importante! Como a borda de é são as duas curvas, e , a integral de linha é desmembrada...
Se queremos a integral de linha em , calculemos essas integrais do lado direito e tá tudo certo (hehe ). Bora?
Passo 6
Em relação à integral de linha primeiro, repare que o problema já deu a solução dessa integral...
Todavia ele nos deus esse resultado com a orientação no sentido anti-horário (lembra que quando não fala nada é porque foi nesse sentido?)
Por isso, como precisamos de no sentido oposto, invertemos o sinal do que ele nos deu...
Passo 7
Em relação a integral dupla agora:
Como
Essa integral aí nada mais é do que a Área da região ...
Essa área pode ser obtida fazendo a área da elipse menos a área da circunferência...
Uma área de uma elipse bonitinha com essa cara é
Como
A área da circunferência de raio é...
Passo 8
Voltando ao teorema de Green...
e substituindo esses resultados paralelos...