Questão 4:
Calcule a integral
quando
- é o círculo .
- é a elipse .
Passo 1
Bem, para resolver essa integral de linha nessa circunferência, existem dois caminhos possíveis:
1º - Resolver pelo método direto.
2º - Resolver pelo Teorema de Green.
Ai você pode pensar, neh: “poxa, o teorema de Green é bem mais fácil, será que ele resolve de fato esse problema?”.
A forma de você responder essa pergunta é averiguando as condições do teorema, bora?
Passo 2
O Teorema de Green:
Exige-nos uma
- curva fechada e delimitando uma região .
- campo sem singularidades.
- curva orientada positivamente.
- curva fechada e delimitando uma região .
- campo sem singularidades.
- curva orientada positivamente.
A primeira condição está sendo satisfeita, afinal a curva é uma circunferência de raio ...
A segunda condição, do campo sem singularidades, essa já temos um probleminha...
Veja que não podemos colocar o ponto no campo dado ! (é o mesmo campo só escrito de maneira mais elegante, ok?)
O que normalmente faríamos nesse caso é remover o ponto problemático com uma circunferência. Então, se você for parar para pensar, não precisamos do teorema de Green aqui nesse item, afinal já temos que calcular uma integral de linha em cima de uma circunferência, sacou? Por isso vamos resolver o problema, com o caso Direto.
Passo 3
Para calcular essa integral de linha do caso direto:
Temos três trabalhos a fazer:
1º - Parametrizar a curva .
2º - Calcular o termo .
3º - Substituir os termos da parametrização no campo de vetores .
Partiu?
Passo 4
Bem, uma boa parametrização para a circunferência de raio e que atende aquela orientação é a comparação com a equação da trigonometria
Ou seja
Onde dá uma volta completa
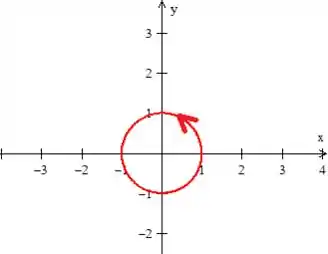
Ou seja, a parametrização é assim
Uma coisa que sempre temos que ter cuidado aqui é com o sentido de giro da curva. Essa parametrização só faz sentido se o sentido de giro dela for o sentido anti-horário, como o problema não nos falou nada, adotamos esse sentido de giro que é considerado padrão, valeu?
Passo 5
Todavia, o que de fato nos interessa aqui é o para encontrar o termo . Bastando então derivar cada entrada de
Então o termo ...
Passo 6
Pegando agora a parametrização e substituindo na função...
Trocando esses e aí pela parametrização, lembrando que
Passo 7
Jogando agora tudo dentro da integral de linha que devemos resolver
Calculando esse produto interno
Epa! Quem é ?
É :D
Passo 8
Agora queremos calcular a mesma integral de linha, mas dessa vez em cima da elipse:
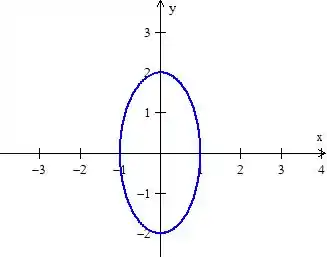
Repare agora que repetir o processo diretão vai dar certo trabalho, pois essa equação da elipse não simplifica muito as coisas.
Dessa vez será legal aplicar o Teorema de Green:
Exige-nos uma
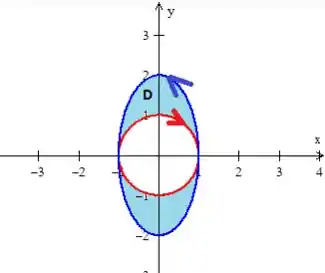
Como já vimos a curva é fechada, mas como o mesmo problema de antes, o campo tem singularidades na origem. Então temos que eliminar esse problema, e vamos fazer isso utilizando uma circunferência de raio , como a do problema do item anterior:
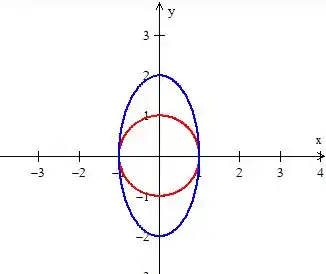
Agora, a região está delimitada por duas curvas: e , onde é a circunferência que adicionamos...
Em relação ao orientada positivamente, como disse, o problema não nos informa isso, então vamos supor que sim:
Passo 3
Condições do Teorema sendo satisfeitas, podemos resolver a integral em , isolando...
Esse sinal em cima da integral de linha em , pode sumir, caso invertemos o sentido de rotação em cima de , ou seja, agora ela girará no sentido anti-horário:
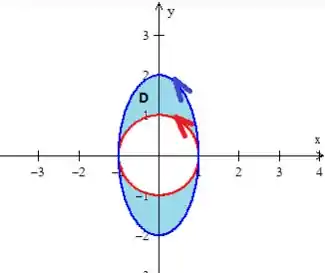
Então...
Passo 4
Cara, a integral de linha em , já foi calculada no item . Ora bolas, pois é a mesma circunferência girando no mesmo sentido, saca?
Então...
Então só nos falta calcular a integral dupla!
Passo 5
Para isso, calculemos...
Primeiro quem são mesmos esse e ?
São os elementos do campo
Calculando então essa primeira derivada parcial
Agora aqui, não podemos esquecer-nos de derivar aplicando a regra da razão
Derivando esses caras do denominador
Passo 6
Fazendo o mesmo, mas agora para :
Passo 7
Opa!!! Deu igual! Isso quer dizer que
Então...
Sacou?! :D