Encontre todos os valores possíveis de
Onde é uma curva fechada qualquer que não passa pela origem.
Passo 1
Bem, como nós não temos muitas informações a respeito da curva (na verdade não temos nenhuma informação), da forma direta não poderemos calcular essa integral de Linha.
Além disso, o fato de a curva ser fechada, a única coisa que podemos fazer é tentar provar que esse campo é conservativo, isso nos dará algumas respostas.
Para fazer essa verificação, calculemos a famosa subtração:
Passo 2
Como
Calculando essas derivas parciais começando por e tendo cuidado com a regra da fração...
Calculando a outra derivada...
Então...
Passo 3
Este Resultado é um tanto quanto interessante, pois essa subtração ser é uma condição necessária para o campo ser conservativo, mas não suficiente!
Precisamos de um domínio simplesmente conexo, ou seja, um domínio onde conseguimos criar curvas fechadas que não contenha pontos problemáticos (singularidades).
Infelizmente, se você olhar novamente para o campo...
Vai notar que ele tem um probleminha na origem, pois se substituirmos e , ganhamos uma divisão por zero o que não pode acontecer:
Passo 4
Então, ao redor do zero, não podemos colocar uma curva fechada de tal forma que o campo é conservativo, mas em qualquer outro ponto fora dele podemos
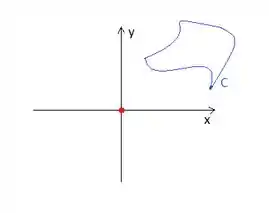
O que significa que se desenharmos uma curva fechada que não contenha a origem, a resultado da integral de linha sobre ela será...
pois é uma consequência de ser um campo conservativo!
Passo 5
Quando a curva engloba a origem, não podemos falar nada ainda, então vamos calcular!
Imagine que essa seja a curva qualquer :
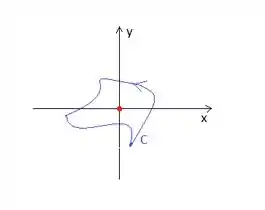
Como não temos informação sobre a curva e já sabemos que aquela subtração é , podemos pensar no teorema de Green:
Mas já sabemos que pra aplicar esse teorema temos que avaliar as condições de Green:
- Uma região fechada sendo delimitada por uma borda .
- Sem singularidades onde estamos trabalhando.
- Curva orientada positivamente.
Passo 6
A curva que temos até é fechada e orientada positivamente, mas ela contém uma singularidade onde estamos trabalhando, logo devemos remover a singularidade com outra curva, mas dessa vez, com uma conhecida: a circunferência de raio ...
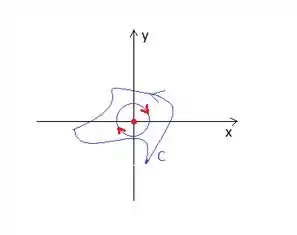
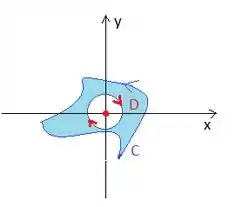
Vamos nomeá-la de , e sua equação é .
Passo 7
Condições do Teorema sendo satisfeita, podemos aplicar a igualdade:
Só que com um detalhe, essa integral de linha está no bordo que no nosso caso é a união da curva com ...
A integral dupla sai facilmente:
Como queremos a integral em ...
Calculemos a integral na curva conhecida e matamos o problema. Só mais um detalhe que simplifica as contas: a curva gira no sentido horário, mas podemos transformar aquele menos em um mais caso invertemos o sentido de giro da curva :
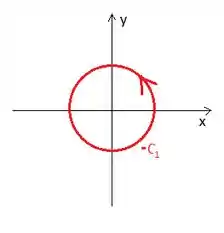
Passo 8
Se vamos calcular essa integral de linha do lado direito, precisamos parametrizar a curva :
Como é uma circunferência...
Onde dá uma volta completa:
Com essa parametrização ela gira para onde queremos que é o sentido anti-horário positivo.
A parametrização de uma forma legal é:
Passo 9
Devemos agora encontrar a derivada da parametrização para determinar o termo fazendo:
Passo 10
Trocando os termos do campo pelos da parametrização...
Lembrando que ...
Substituindo tudo na integral de linha:
Então dois outros prováveis resultados para a integral de linha em que contém a origem é
Esse último positivo é dado, pois poderíamos girar na curva o sentido horário por exemplo, saca? Nesse caso invertemos o sinal