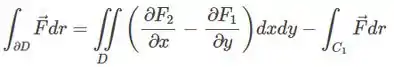Seja a fronteira da região de limitada por e , percorrida uma única vez no sentido anti-horário. A integral é igual a:
Passo 1
Bom, você já deve ter notado que tentar resolver aí pelo método direto irira ser meio complicado. Mas, pra nossa sorte, existe o teorema de green.
O teorema nos diz:
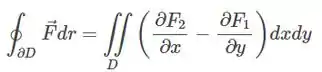
Aonde seria a fronteira da região limitada por e .
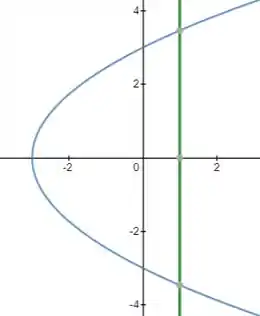
No entanto, se você for observar, no x=0 e y=0 existe uma singularidade no campo. Por isso, vamos excluir a singularida com a melhor figura.
Se você se lembra bem, quando escolhermos a curva para excluir a singularidade, vamos ficar com:
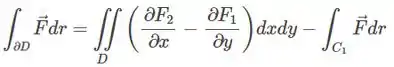
Aonde vai ser a integral de linha em cima dessa curva escolhida. Ou seja, vamos ter ainda que calcular uma integral de linha pelo método direto. Por essa razão, vamos escolher uma curva que facilite nossa vida. Se você for observar, no denominador do nosso campo temos logo, pra facilitar nossos passos, vamos escolher .
Ficaremos então com:
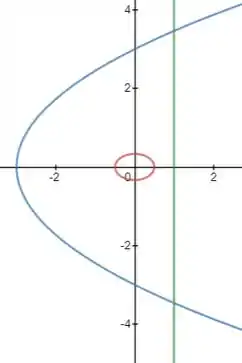
Vale lembrar que, como nossa cusva gira no sentido anti-horario, a curva deverá girar no sentido oposto.
Passo 2
Iniciando os cálculos com a intetegral dupla ficamos com:
Logo:
Opa!! Isso zera toda nossa integral dupla! Então podemos já partir para integral de superfície em cima da elipse.
Passo 3
Começamos então parametrizando:
Observe que escrevi variando de até 0, para mantermos uma orientação positiva, com a elipse girando no sentido horário!
Termo ds:
Escrevendo o cmapo em função da parametrização ficamos com:
Montando então a integral:
Passo 4
Voltando então ao teorema ficamos com: