24) Calcule
Onde é a curva , , orientada de à
Passo 1
Bem, sabemos que uma integral de linha com essa cara
Nada mais é do que uma integral de linha a qual estamos acostumados...
Onde:
O campo não parece legal o que já sugere o Teorema de Green, mas para termos certeza... Calculemos:
Passo 2
Calculando primeiro a primeira derivada parcial, , e tomando cuidado com a regrada da fração vamos obter...
Agora a segunda, ...
Portanto:
Ótimo! Simplificou muito a vida, então podemos pensar no Teorema de Green!
Passo 3
O teorema de Green nada mais é do que essa igualdade mara entre a integral de linha com uma integral dupla:
Mas antes de aplicarmos essa igualdade maravilhosa do Teorema, temos que avalizar as condições de Green, que sempre nos exige:
1º - Uma região fechada que tem com borda, a curva fechada .
2º - Um campo sem singularidades onde estamos trabalhando.
3º - Orientadas positivamente.
Vamos averiguar?
Passo 4
O primeiro, como vimos, nos diz que precisamos de uma curva fechada e delimitando uma região .
Ora, a curva , pelo próprio enunciado, é fechada e a elipse...
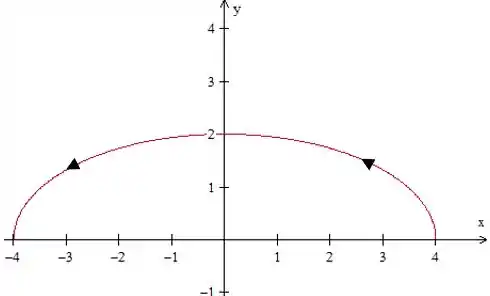
Repara que a curva não é fechada, para aplicarmos o teorema de Green devemos fechar essa curva.
Mas aqui temos um problema: o campo não está definido em toda a região dentro da elipse ferindo a segunda condição. Se substituirmos na função teremos zero no denominador!
O que faremos então?
Nós tiraremos a origem da jogada com uma circunferência!
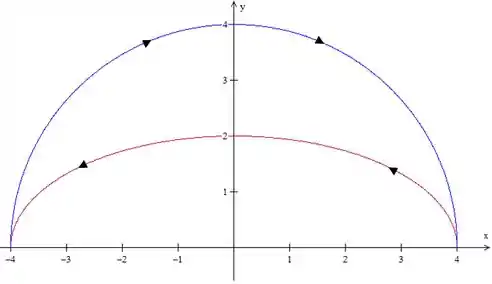
Essa circunferência de raio ,
que vamos chamar de , delimita uma lua como região, e essa lua não passa pelo ponto problemático saca?
Passo 5
Quanto ao orientada positivamente, não está ok, pois o bordo de gira no sentido horário!
Podemos corrigir esse detalhe, mudando o sinal da integral dupla na fórmula de Green...
Agora, com essas condições estando ok, essa integral é muito útil. O único detalhe é que a integral de linha, calculada na borda, deve ser desmembrada em duas partes: uma em cia da circunferência e a outra em cima de :
Só mais uma simplificação... Podemos eliminar esse sinal negativo na frente dessa integral de linha caso invertemos o seu sentido para o anti-horário, representado por :
Se queremos essa integral em cima de , calculemos essas integral do lado direito e tá tudo certo!
Passo 6
Calculemos aqui primeiro essa integral dupla:
A primeira integral representa:
Como ...
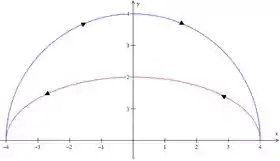
A área de vai ser a área da semicircunferência menos a da semielípse (), ou seja...
No nosso caso o raio da circunferência é enquanto que a elipse é ...
Passo 7
Em relação a essa outra integral aí:
Bem, como estamos calculando uma integral em uma região simétrica e relação ao eixo ...
e a função que estamos integrando é ímpar (), então sua integral dupla será...
Se quiser conferir, basta montar a integral dupla descrevendo como do tipo onde:
Enquanto o , vai da elipse à circunferência:
Passo 8
Agora vamos para a integral de linha que adicionamos ao problema...
em cima da semicircunferência:
- Precisamos dela parametrizada e como é uma circunferência de raio ...
- O termo é...
- Não se esqueça de trocar os termos da função ...
ou
como estamos dando uma semi-volta volta completa...
Se você se lembrar de que pegamos a circunferência ...
Substituindo na integral de linha...
Vamos separar essa integral em duas
Passo 9
Começando com
Lembrando que
Voltando...
Passo 10
Indo para a segunda integral
Fazendo uma mudança de
Mudando os limites também...
Como a função é contínua, nem precisa terminar a conta, pois...
Logo...
Passo 11
Retornando ao teorema de Green...
E substituindo os dois resultados que encontramos...