3) Calcule , onde e
Passo 1
Bem, antes da mais nada, separaremos essa função em duas...
Onde...
Então...
Passo 2
Primeiro vamos resolver o problema para que parece ser menos chata...
Hmmmm, o problema até nos deu a curva já parametrizada, mas será que resolver a integral de linha ainda de uma forma direta seria uma boa?
A resposta é não. Afinal de contas, essa parametrização com essa parametrização ficaria um seno dentro de um próprio seno. Por isso, vamos buscar uma alternativa.
Essa alternativa é... O teorema de Green, afinal de contas...
Simplifica a nossa vida. Vamos calcula-lo?
Logo...
Olha que resultado bonito, senhoras e senhores! Indicando que sim, vamos usar o Teorema de Green! :D
Passo 3
O teorema de Green...
Mas antes de aplicar a igualdade, devemos averiguar certas condições:
1º - Uma região sendo delimitado pela superfície borda .
2º - Um campo sem singularidades onde estamos trabalhando.
3º - Uma orientação positiva.
Passo 4
Infelizmente, caso desenhemos a curva , nos representa uma semicircunferência de raio ...
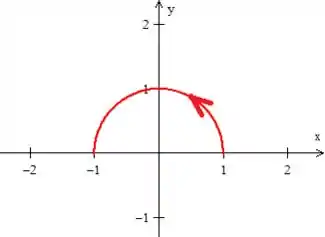
Como precisamos de uma região fechada, a fecharemos com uma reta , que chamaremos de ...
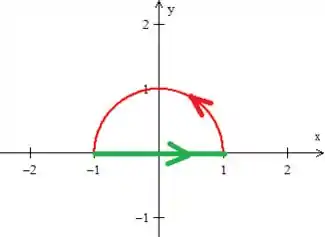
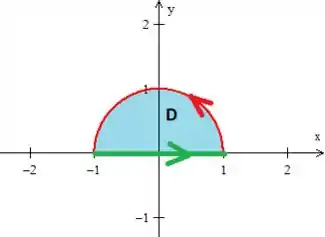
Esse campo , não apresenta singularidades como uma divisão por , ou algo do tipo.
Quanta a terceira condição, observe que elas estão orientadas no sentido positivo já que ambas giram no sentido anti-horário.
Logo, pelo Teorema...
Como a borda de é e ...
Bora calcular essa integral?
Passo 5
Parametrizando a curva ...
Onde , vai de até .
Calculando o termo ...
E substituindo no campo os termos da parametrização...
Logo...
Passo 6
Agora, vamos calcular a outra integral de linha
Lembrando que chamamos de ...
Vamos então calcular essa derivada de frações tomando cuidado na hora da regra da fração:
Calculando a outra...
Então...
Indicando que sim, vamos usar o Teorema de Green novamente! :D
Passo 7
Já sabemos que a curva é aberta e que precisamos fecha-la. Anteriormente, fechamos com uma reta, mas será que agora pode ser a reta?
Bem, vejamos a segunda condição: ela nos exige que tenhamos um campo sem singularidades onde estamos trabalhando...
Oh-ouh! O campo apresenta uma singularidade justamente em cima da reta que havíamos pegado, no . Por isso não a poderemos usar como curva novamente.
Vamos usar então a curva , pois ela simplifica o denominador, ao mesmo tempo ela pula o problema:
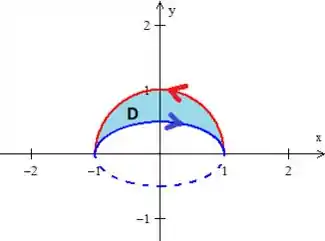
A chamaremos de . Observe que a borda de é a curva e a curva ...
A última condição está sendo satisfeita, a final estão tudo girando no sentido anti-horário.
Passo 8
Aplicando então a igualdade a ferro e fogo...
Podemos mudar esse sinal menos se invertermos o sentido de giro da curva , para (sentido anti-horário ou o oposto ao que já estava):
Passo 9
Então calculemos a integral de linha...
Primeiro parametrizando a curva ...
Comparando com ...
Enquanto dá uma meia volta...
Encontrando o termo ...
Substituindo por fim a expressão de ...
Passo 10
Voltando para a integral geral...