Questão 4: Calcule onde é a fronteira do retângulo percorrida uma vez no sentido anti-horário e
Passo 1
Bem, para termos uma noção clara de como vamos resolver essa integral de linha, primeiro vamos fazer um esboço dessa curva ...
O próprio problema nos disse que ela é esse retângulo , que desenhado no plano...
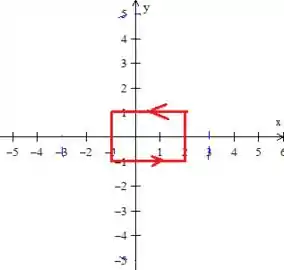
e esse cara aí!
Agora, vai ser muito chato calcular a integral desse campo, que não é nada bonito, em cima dessa curva, por isso, vamos pensar no teorema de Green
Passo 2
Para termos certeza que vamos aplicar o teorema, calculemos:
Como...
Calculemos essa primeira derivada aí:
Aplicando a regra da fração...
Calculando a segunda derivada com contas extremamente semelhantes...
Aplicando a regra da fração...
Logo...
Subtração mais easy que essa... Só duas dessa
Passo 3
O teorema de Green nada mais é do que essa famosa igualdade:
Onde esse é a borda da região fechada , saca?
Bem, mas é claro que não podemos aplicar essa igualdade assim... Do nada. Precisamos analisar as condições do teorema:
1º - Temos que ter uma curva fechada delimitando .
2º - deve estar orienta positivamente!
3º - Precisamos de um campo sem singularidades onde estamos trabalhando.
Vamos ver se no nosso caso, cada um desses itens é satisfeito? Então me acompanhe! :D
Passo 4
1º - Temos que ter uma curva fechada delimitando .
Sim, isso já acontece. Onde, nesse caso, a borda coincide com a curva :
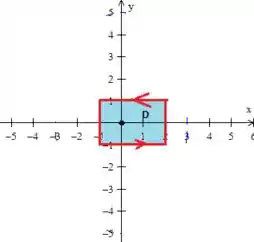
2º - deve estar orienta positivamente!
Isso também acontece, pois a curva está girando no sentido anti-horário.
3º - Precisamos de um campo sem singularidades onde estamos trabalhando.
Opssss! Isso não acontece, pois se você olhar novamente para o campo:
você vai notar que quando estamos na origem, com e , o campo dá uma divisão por zero o que sabemos que não pode acontecer. E a região que estamos trabalhando, contêm esse ponto:

Por isso, devemos colocar outra curva ao redor desse ponto eliminando o nosso problema!
Passo 5
Escolhendo a curva que elimina a singularidade...
Bem, como podemos escolher, será de grande ajuda se escolhêssemos uma curva que de quebra simplificasse esse campo
Repare que o denominador dele é bem característico... . Essa equação nos lembra uma elipse certo? Então vamos pegar uma elipse !
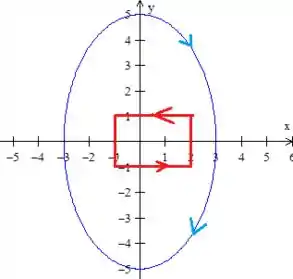
Essa elipse aí simplifica as coisas, mas o problema é que ela é grande demais (até poderia, mas vai ficar mais confuso).
Por isso, vamos reduzi-la:
Pronto! Essa elipse é a mesma da de cima só que reduzida, saca?
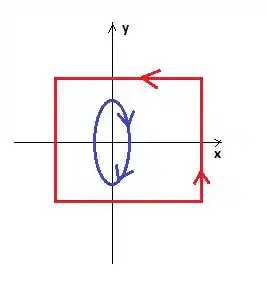
Passo 6
Bem, note que agora a borda da região fechada é a curva e essa curva aí que vamos chamar (ela necessariamente tem que girar no sentido contrário a curva vermelha):
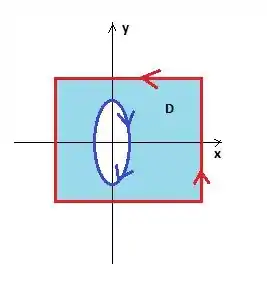
Se a borda é duas curvas... Desmembramos a integral de linha na borda em duas integrais:
Como ...
Ou seja... a integral de linha que a gente quer em cima de é o negativo da integral mais fácil em cima dessa elipse orienta no sentido horário!
Podemos simplificar ainda mais se colocando um mais ali seeee invertermos o sentido da elipse (representado por )!
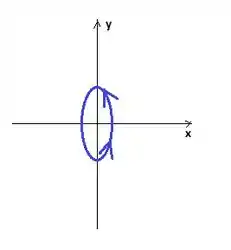
Então vamos calcular essa integral de linha do lado direito e ser feliz
Passo 7
Para resolver essa integral de linha:
precisamos parametrizar a elipse...
Se colocarmos essa elipse na sua forma geral de elipses, ou seja
a parametrização é:
Então...
Então...
Ou, melhor dizendo:
Onde o dá uma volta completa...
Passo 8
Para o termo , calculemos:
Calculando a derivada...
logo...
Passo 9
Não podemos de deixar de passar o campo vetorial para os termos da parametrização:
lembre-se que ...
Passo 10
Regressando à integral de linha que queremos resolver:
e substituindo os ingredientes...
Como
então, essa integral de linha é...