Seja
Calcular a integral de linha vetorial , onde é a curva união das curvas planas e :
é a fronteira do quadrado orientada no sentido anti-horário
é a fronteira do quadrado orientado no sentido horário
Passo 1
Bom, o enunciado é bem grande, mas na verdade mesmo o que ele quer é a integral de linha
Onde na verdade são duas curvas, então
Vai dar um trabalho tentar fazer isso da forma direta, não é? Até porque nosso campo é bem complicado também, vamos tentar usar o teorema de Green aqui!
A nossa curva tem esse esboço aqui
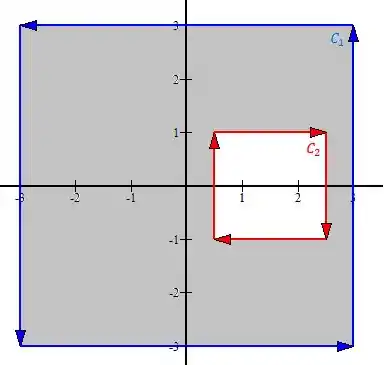
Perceba que já colocamos a região do teorema de Green aqui, nela percebemos um problema: o campo possui uma singularidade em , porque o denominador fica zero! Então pra usar o teorema de Green aqui vamos ter que excluir esse ponto.
Beleza, mas qual a melhor curva pra excluir o ponto?
Bom, aqui vamos escolher uma circunferência , onde . Escolhemos essa curva porque o denominador do campo é exatamente , então fica simples de calcular tudo depois.
Resumindo, o nosso novo esboço fica assim
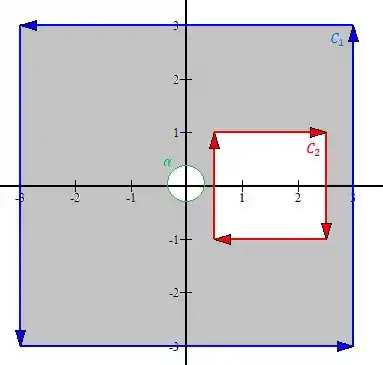
Note que excluímos a singularidade e, para isso, a orientação da curva deve ser no sentido horário, nunca se esqueça de conferir a orientação da curva, ta bem?
O teorema de Green fica
Passo 2
Vamos começar calculando essa integral dupla do teorema. Pra isso precisamos derivar o campo .
Agora derivando
Portanto a integral dupla fica
Bem mais fácil assim né? Bom, voltando pro nosso esboço, qual é a área de toda aquela região cinza?
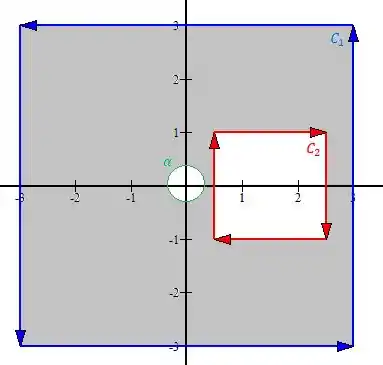
A área de é a área do quadrado de lado , logo
A área de é a área do quadrado de lado 2, logo
A área de é a área de um círculo de raio , logo
Passo 3
Pra terminar a questão ainda falta calcular a integral da curva que acrescentamos, ou seja, a integral de .
Pra isso precisamos parametrizar a curva. Como se trata de uma circunferência, temos
Onde
Só que queremos a orientação horária de , certo? Então vamos inverter esses limites aí na integral, beleza?
Fazendo a integral de linha diretamente, precisamos derivar a parametrização da curva, lembra?
O campo fica assim
Juntando tudo na integral
Pra integrar isso aí, sabemos que
Logo
Passo 4
Agora temos tudo, só juntar no teorema de Green lá do passo 1