Seja uma curva parametrizada por , por partes como no esboço abaixo tal que e . Calcule
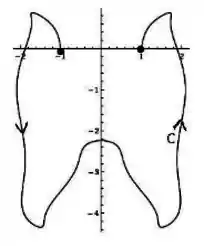
Passo 1
Como não temos a equação dessa curva para calcular a integral de linha pela definição, vamos aplicar o Teorema de Green.
Como a curva não é fechada, precisamos criar uma curva que ligue os pontos e , que chamaremos de . Perceba que o campo vetorial não está definido na origem , pois teríamos zero no denominador, assim, não pode ser uma reta. Mais à frente veremos que curva será essa. Orientando positivamente as duas curvas, teremos, então:
Passo 2
O campo vetorial pode ser escrito como
Vamos agora calcular :
Passo 3
Aplicando o teorema de Green, temos:
Passo 4
Agora precisamos resolver a integral ao longo de , mas que curva será essa? Já que não podemos escolher uma reta, vamos ver que expressão poderia simplificar nossas contas. Veja que nas duas componentes do campo vetorial, temos o termo no denominador, que se assemelha à expressão de uma elipse.
Se escolhermos a parte com da elipse para ser essa curva, teremos para sua parametrização, certo? Com variando de até para a orientação ser positiva. Veja que a origem está fora da região limitada pelas curvas.
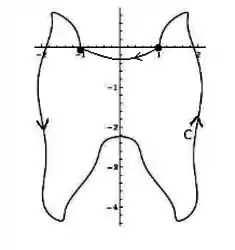
Assim, teremos nos denominadores, o que simplifica bastante.
Passo 5
Agora vamos calcular :
Passo 6
Substituindo esses valores na fórmula
Temos:
Passo 7
Agora vamos resolver essa integral:
Passo 8
Como temos
A integral que buscamos será