Use o teorema de Green para calcular a integral de linha
Em que é a curva mostrada abaixo, orientada no sentido anti-horário e dada por
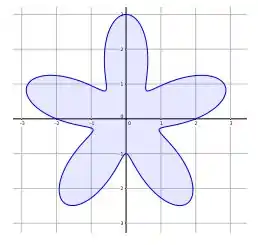
Passo 1
Para começar, relaxa! Não vamos trabalhar com essa estrala do mar aí de forma alguma! Isso é só para tentar nos atrapalhar, mas não vai sabe por quê?
Porque esse campo tem um problema na origem!
Veja que não podemos colocarmos o ponto no campo dado ! (é o mesmo campo só escrito de maneira mais elegante, ok?)
Logo, para aplicar , vamos ter que circular esse ponto com uma bola de raio qualquer!
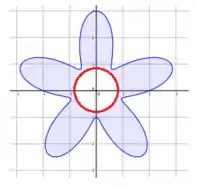
Para facilitar as contas, vamos pegar o raio valendo , beleza?
Ahhh! E vamos nomear essa curva de !
Passo 2
Bem, antes de aplicar o teorema de , nos devemos nos atentar a um detalhe: Qual é a orientação da curva vermelha?
Bem, sabemos que para aplicar a curva de fora deve estar girando no sentido anti-horário, o que já acontece. Logo a curva de dentro deve estar girando no sentido contrário:
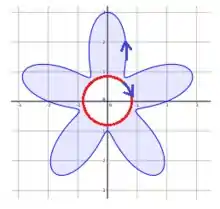
Agora que estamos nas condições, vamos aplicar ...
Ou seja, a integral na borda de uma região (no caso são essas duas superfícies ), é a integral dupla do rotacional desse campo !
Podemos separar essa integral do lado direito em
Bem, então basta calcular essas duas outras integrais aí, e pronto!
Partiu encontrar esse rotacional então?
Passo 3
Primeiro quem são mesmos esse e ?
São os elementos do campo
Calculando então essa primeira derivada parcial
Agora aqui, não podemos esquecer-nos de derivar aplicando a regra da razão
Derivando esses caras do denominador
Passo 4
Fazendo o mesmo, mas agora para :
Opa!!! Deu igual! Isso quer dizer que
Passo 5
Voltando então para
E quem é essa integral de linha do lado de lá?
É a integral de linha sobre a circunferência que colocamos no problema, porém o sinal indica que devemos tomar ela girando pro outro lado:
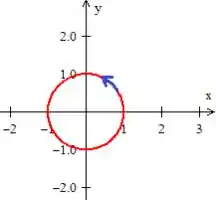
Como trocamos o sentido da curva, esse menos desaparece
Bem, agora não tem por onde fugir! Devemos parametrizar essa curva aí e integrar direto, bora?
Passo 6
Bem, uma boa parametrização para a circunferência de raio e que atende aquela orientação é a comparação com a equação da trigonometria
Ou seja
Onde dá uma volta completa
Ou seja, a parametrização é assim
Bem, mas o que de fato nos interessa aqui é o , bastando então derivar cada entrada de
Passo 7
Jogando tudo dentro da integral de linha que devemos resolver
Trocando esses e aí pela parametrização, lembrando que
Calculando esse produto interno
Epa! Quem é ?
É :D
Passo 8
Retornando para , recordamos que...
Portanto