Considere o campo vetorial no plano dado por
Calcule a integral de linha , onde é a parte da elipse contida no primeiro quadrante, com ponto inicial e ponto final .
Passo 1
Vamos começar o nosso problema entendendo um pouco melhor quem é a curva e como podemos chegar no resultado.
A curva é formada por uma elipse com o eixo maior sobre , pois se a gente lembrar da configuração geral dessa elipse: com ; e comparar com a que nós temos, vamos perceber que que é maior que . Logo
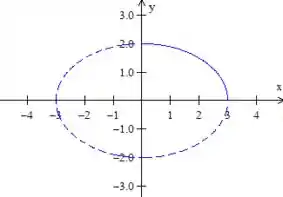
Note que não queremos a elipse toda e sim apenas esse pedaço no primeiro quadrante. :)
Passo 2
A gente poderia tentar resolver pelo método direto, porém note que daria um certo trabalho para substituir naquela função bizarra!
Ao invés disso, vamos tentar aplicar Green que nos fala que a integral de linha do bordo de uma superfície fechada é a integral do rotacional, dessa forma aqui:
Lembrou?!:D
Ok! E quem é mesmo esse bordo ? É a borda dessa superfície fechada aqui
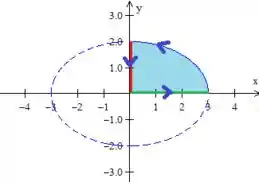
Logo, como a borda é formada pela união de três curvas, a em azul, a em vermelho e em verde, teremos para aplicar o nosso amigo Green
Bem, agora é só calcular essas três integrais aí, que eu prometo ser mais simples que calcular esse integral direto. Bora lá?!
Passo 3
Vamos então começar com essa integral dupla aí. Lembrando que esse é a primeira entrada do vetor e é a segunda, ou seja, , teremos então
Então, o rotacional que é nos dará
Essa resultado aí nos diz que essa integral dupla é três vezes o valor da área da região . Pois então, a área dessa região é da área total dessa elipse
Se lembra daquele bizu da área da elipse (área produto dos eixos por , ou melhor, )? Se a gente tem aqui que e , então
Ou seja,
Passo 4
Falta agora resolver aquelas duas integrais de linha. Mas relaxa que elas são mais simples pois as “linhas”, ou melhor, as curvas e são mais fáceis de parametrizar, veja só
- é uma reta que tem e está indo de até , logo, podemos parametrizar
- Enquanto que é uma reta que tem e está indo de até , logo, podemos parametrizar
Onde e
Onde , e
Pois bem, vamos resolver essas integrais de linha separadamente, okay?
Passo 5
Começando pela , devemos obter o termo
Derivando a curva em relação a
Logo
Agora aplicando na integral de linha
E resolvendo esse produto escalar:
Epa!!! Estamos integrando em , logo devemos substituir a nossa parametrização nessa função, ou seja, como , e
Fazendo uma substituição simples do tipo , , enquanto que os limites, quando e
Substituindo os limites
Passo 6
Repetindo o processo para
Substituindo a parametrização de da curva
Passo 7
Voltando para Green...
Isolando , obteremos
Resposta
Exercícios de Livros Relacionados
Ver Mais
Ver Mais
Ver Mais