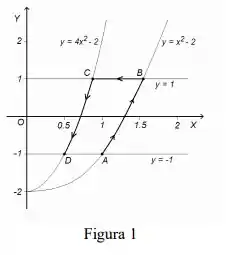
Questão um: utilizando o teorema de Green, calcular o valor da integral de linha do campo vetorial sobre o contorno aberto , definido na Fig. , com ponto inicial e ponto final .
Passo 1
Pelo próprio item da questão, sabemos que vamos ter que utilizar o teorema de Green para atacar o nosso problema. Então nada mais justo que aplicarmos a fórmula do teorema!
Nessa integral temos que saber que é a uma curva fechada que delimita a região , e ora bolas, a curva fechada é essa daqui, oh:
Saca?
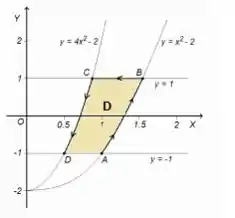
Mas olha, tenho de te alertar para tomar cuidado, pois o exercício não quer o valor da integral de linha em cima da fechada, por isso, dividimos a curva fechada em duas:
Repare que é a “soma” da curva azul (a curva , que o problema quer) com a curva vermelha que ...Logo:
Se buscamos a integral de linha em ...
Então é só calcular essas duas integrais aí e correr para o abraço! Vamos nessa?!:D
Passo 2
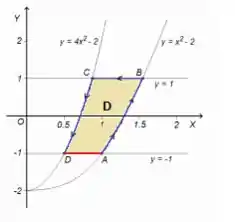
Vamos começar aqui com essa integral de linha em cima da reta vermelha que surgiu:
Aqui não tem truques, tem que ser calculada de uma forma direto, por isso, a primeira coisa que fazemos é a parametrização de :
é uma reta que tem sempre e o variando... Então uma boa parametrização é...
A parametrização arrumadinha é:
Como varia de até ...
Note que com essa parametrização, a reta vermelha é formada no sentido de giro da curva... Isso é importante !
Passo 3
Agora precisamos do termo ...
Derivando a curva...
Passo 4
Como, já sabemos, temos que trocar os termos do ...
e ...
Passo 5
Substituindo tudo então na integral de linha que estamos trabalhando
Não se esqueça de que esse é os limites do parâmetro...
Calculando esse produto escalar de vetores...
Passo 6
Muito bem, não desanima, mas ainda temos que buscar o resultado da outra integral, a dona integra dupla:
Para a resolução dela, antes temos que saber que função é essa aí que está na integral:
Pra isso basta pegar o campo...
e calcular essas derivadas parciais:
A primeira derivada parcial é e a segunda devemos aplicar a regra da fração:
Quanto à segunda derivada parcial...
Aplicando a subtração ganhamos:
Logo:
Passo 7
Agora repare que usualmente descreveríamos a região para concluir a integral dupla, mas no nosso caso...
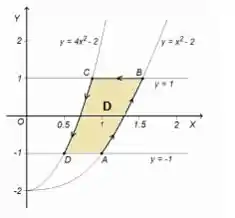
A região é extremamente complexa para fazermos isso!
Ok, essa não é saída, mas se você reparar, aquelas parábolas são bem parecidas e mais: dentro da integral , tem um , também bem parecido com as equações das parábolas, percebeu?
Então podemos realizar uma mudança de variáveis quaisquer para matar o nosso problema! :)
Para encontrar os limites de , basta trabalhar com as duas parábolas:
Epa! Então ...
Como sabemos, uma mudança dessas necessita de outra variável, a , mas se reparamos na região , as outras duas retas com que delimita , está ok, então:
E o limite será o próprio limite de :
Passo 8
Você não pode se esquecer de que uma mudança dessas sempre deixa marcas, e essa marca nós corrigimos com o calculo do Jacobiano. Como temos aqui as novas variáveis em função das antigas:
Fica mais fácil calcular o Jacobiano inverso primeiro:
Calculando cada uma dessas derivadas parciais:
Logo:
O Jacobiano tem uma relação muito legal com o seu inverso... Ele é o inverso :
Lembre-se de que precisamos na real é a do módulo heim!
Passo 9
Finalmente, com as informações de variação das nossas variáveis:
Podemos voltar para a integral dupla:
E substituir tudo, não se esquecendo de multiplicar pelo módulo do Jacobiano que encontramos:
Passo 10
Calma! Ainda não acabou! Precisamos retornar ao teorema de Green:
E substituir os dados que encontramos:
Dando que a integral de linha na curva é... UFA!!!