Exercícios de Estabilidade - Lista de Exercícios Resolvida
Questão 1
Ao flutuar em água , um corpo triangular equilateral pode assumir uma das duas posições mostradas na Figura abaixo. Qual é a posição mais estável? Considere que a largura seja grande normal ao papel.
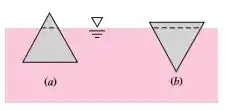
Questão 2
Descreva os 3 diferentes tipos de equilíbrio de um corpo parcialmente submerso em um fluido. Quais as condições para que eles aconteçam?
Ver solução completaQuestão 3
Um corpo flutuante será estável quando:
o seu centro de gravidade estiver acima de seu centro de empuxo;
o centro de empuxo estiver abaixo da linha d’água;
o centro de empuxo estiver acima do seu metacentro;
o metacentro estiver acima do seu centro de empuxo;
o metacentro estiver acima do seu centro de gravidade.
Ver solução completaQuestão 4
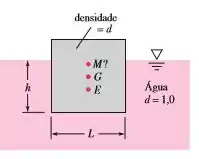
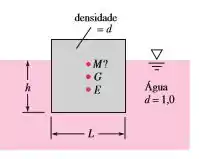
Um iceberg pode ser idealizado como um cubo de lado , como na Figura abaixo. Se a água do mar for representada por , então o gelo da geleira (que forma os icebergs) tem . Determine se esse iceberg “cúbico” é estável para a posição mostrada na Figura abaixo:
Questão 5
Considere um cilindro de madeira () de 1 m de diâmetro e 0,8 m de comprimento. Esse cilindro seria estável se colocado para flutuar com seu eixo na vertical em óleo ()?
Ver solução completaQuestão 6
Uma barcaça tem de largura e de comprimento e flutua com um calado de . Ela recebe uma carga de cascalho tal que seu centro de gravidade está acima da linha d’água. Ela é estável?
Ver solução completaQuestão 7
(Adaptada) Considere um cone circular reto uniforme de densidade , flutuando com seu vértice para baixo na água (). O raio da base é e a altura do cone é . Calcule e verifique se esse cone é estável para a altura submersa .
Dados: e .
Ver solução completaQuestão 8
A idealização do iceberg do problema anterior (cubo de lado L parcialmente imerso na água do mar) pode se tornar instável se seus lados derreterem e sua altura exceder sua largura. Na Figura considere que a altura seja L e a profundidade normal ao papel seja L, mas a largura no plano do papel seja . Considerando para o iceberg, encontre a razão para a qual ele se torna neutramente estável (isto é, prestes a emborcar).