Exercícios de Potencial Elétrico Gerado por Corpos Extensos - Lista de Exercícios Resolvida
Questão 1
Uma camada semiesférica isolante de raio interno e externo tem uma densidade volumétrica de carga que decresce com o inverso da distância ao centro segundo .
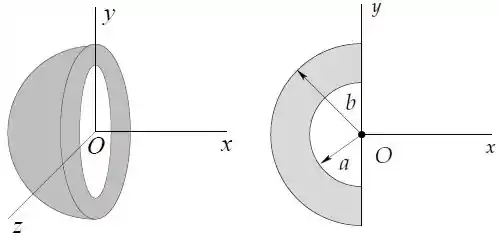
Dados e .
- Determine a carga total da camada semiesférica.
- Determine o potencial elétrico no ponto da cama semiesférica. Adote potencial nulo no infinito.
- Se uma carga pontual com o mesmo sinal da constante da densidade volumétrica de carga é solta no centro , qual é a velocidade final que ela atinge?
Questão 2
A figura à seguir mostra esquematicamente uma seção transversal de um objeto condutor maciço (de carga elétrica total nula) colocado em um campo eletrostático externo, após atingido o equilíbrio eletrostático.
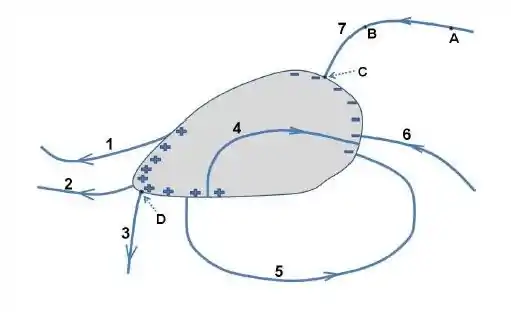
Algumas das linhas de campo elétrico, parcialmente desenhadas na figura, estão erradas e não podem corresponder a uma situação física real. Assinale a seguir cada linha impossível.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
[Atenção: nesta questão pode haver mais de um item correto].
Ver solução completaQuestão 3
Considere um anel não-condutor situado no plano de raio interno e raio externo com uma densidade superficial de carga uniforme , como pode ser observado na figura.
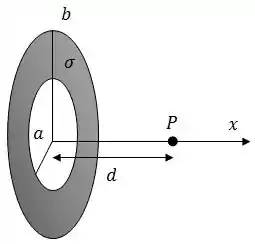
Calcule o potencial elétrico gerado por esta distribuição no ponto , a uma distância sobre o eixo indicado na figura.
A partir do resultado do item , encontre o campo elétrico (modulo, direção e sentido) no ponto .
Calcule o trabalho realizado para trazer uma carga puntiforme do infinito até o ponto .
Ver solução completaQuestão 4
Um cilindro condutor infinito ao longo do eixo de raio tem densidade de carga constante . Calcule o potencial a uma distância do eixo do cilindro, dado que a uma distância ele vale . O potencial dado poderia ter sido no infinito?
Ver solução completaQuestão 5
Uma esfera condutora de raio e com carga é envolta por uma camada esférica isolante de raio interno e externo com densidade de carga volumétrica constante.
Determine o vetor campo elétrico em todo o espaço;
Determine o potencial elétrico em todo o espaço. Adote potencial nulo no infinito;
Ver solução completaQuestão 6
Dado uma esfera condutora de raio e carga envolta por uma casca esférica condutora neutra de raios interno e externo iguais a e . Dado que o potencial no infinito é nulo, calcule o potencial em cada região:
Questão 7
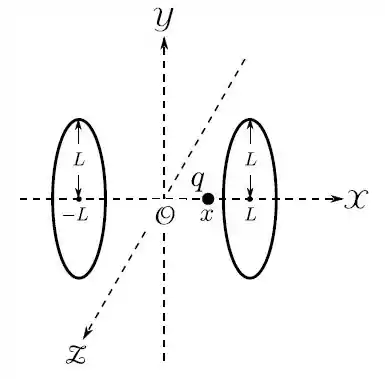
Dois anéis circulares, de mesmo raio , perpendiculares ao eixo , tem seus centros em e . Ambos possuem a mesma carga total , uniformemente distribuída.
- Determine o potencial elétrico devido aos anéis, em um ponto genérico do eixo , com abscissa , tomando tal potencial como zero no infinito ().
- Usando o potencial do item (a), determine o campo elétrico devido aos anéis, no mesmo ponto supracitado.
- Considere agora uma partícula de carga , ainda no mesmo ponto supracitado. Determine a energia potencial associada à interação dessa partícula com o campo elétrico produzido pelos anéis!
Questão 8
Considere um disco de raio carregado uniformemente com carga . Calcule o potencial elétrico ao longo do eixo a uma distancia do centro do disco. Adote potencial nulo no infinito.
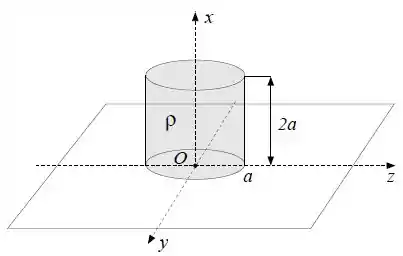
Calcule o potencial elétrico no ponto com coordenadas devido a um cilindro de altura e raio de base , uniformemente carregado com densidade volumétrica de carga . A base do cilindro está contida no plano e seu eixo coincide com o eixo , conforme a figura. Sugestão: Decomponha o cilindro em discos elementares de altura e utilize o resultado do item (a).
Questão 9
Um fio retilíneo fino, de comprimento , está postado ao longo do eixo cartesiano , com seu centro na origem desse. A densidade linear de carga de tal fio é dada por:
Onde .
- Calcule o potencial eletrostático para um ponto arbitrário no eixo cartesiano , com ordenada . Faça, como usual, o potencial igual a zero no infinito [Sugestão: lembre-se que, para temos simplesmente ao passo que para temos ].
- Calcule, agora, a componente do vetor campo elétrico em tal ponto;
- Determine, por fim, a carga total de tal fio.
Questão 10
A figura abaixo mostra três arcos de circunferência não-condutores de raio .
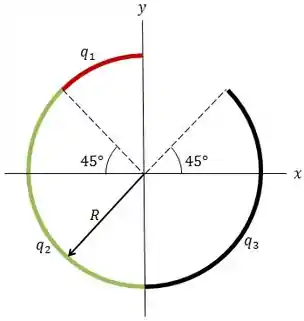
As cargas dos arcos são , e . Com no infinito, qual é o potencial elétrico dos arcos no centro da curvatura?
Ver solução completaQuestão 11
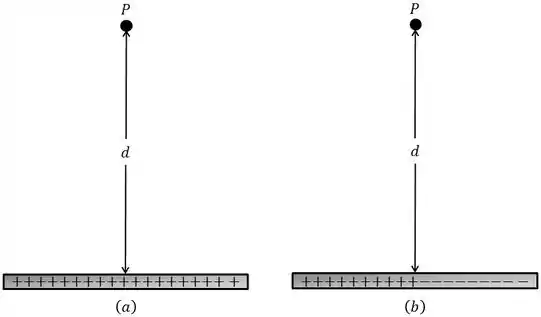
- A figura a seguir mostra uma barra não-condutora de comprimento e densidade linear de cargas positiva uniforme . Tome no infinito.
Qual é o valor de no ponto situado a uma distância acima do ponto médio da barra?
- A figura mostra uma barra idêntica à do item , exceto pelo fato de que a metade direta agora está carregada negativamente;
Qual é o valor de no ponto situado a uma distância acima do ponto médio da barra?
O valor absoluto da densidade linear de cargas continua a ser em toda a barra. Com no infinito, qual o valor de no ponto ?
Questão 12
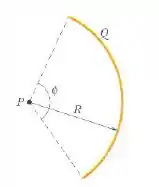
Uma barra de plástico com uma carga uniformemente distribuída tem a forma de um arco de circunferência de raio e um ângulo central . Com no infinito, qual é o potencial elétrico no ponto , o centro de curvatura da barra?
Questão 13
Uma placa condutora infinita possui uma densidade superficial de cargas
(a) Qual é o trabalho realizado pelo campo elétrico produzido pela placa se uma partícula de carga é deslocada da superfície da placa para um ponto situado a uma distância da superfície da placa?
(b) Se o potencial elétrico é definido como sendo zero na superfície da placa, qual é o valor de no ponto ?
Ver solução completaQuestão 14
A figura ilustra uma coroa circular disposta no plano , centrada na origem, de raio interno e raio externo . Sua carga está uniformemente distribuída e possui . Use ou .
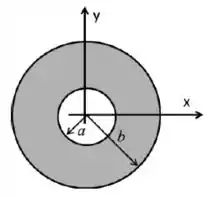
Considerando a referência para potenciais no infinito, encontre o valor do potencial elétrico num ponto qualquer do eixo , à distância da origem.
Calcule o potencial no ponto e o valor do trabalho realizado pela força eletrostática no deslocamento de uma carga teste desde até o ponto onde o potencial vale .
Suponha que o potencial gerado pela coroa circular no ponto tenha valor . Queremos anular o potencial em , e para isso dispomos de uma carga pontual de valor . Determine todos os pontos do espaço em que podemos posicionar a carga de modo a tornar nulo o potencial em .
Ver solução completaQuestão 15
Determine (a) a carga e (b) a densidade superficial de cargas de uma esfera condutora de de raio cujo potencial é (tomando no infinito).
Ver solução completaQuestão 16
O eixo de um cilindro condutor de de raio dista do plano conforme a figura. O cilindro é infinito na direção perpendicular ao plano da figura e todo o semiespaço é preenchido com um material condutor.
O potencial eletrostático num ponto de coordenadas no espaço fora dos condutores é dado por
onde e são em metros.
Determine o potencial no ponto do eixo do cilindro condutor .
Determine o vetor campo elétrico em todo o espaço, inclusive no interior dos condutores.
Ver solução completaQuestão 17
Uma casca esférica condutora de raio interno e externo é concêntrica a uma casca esférica condutora fina de raio . A casca esférica fina tem uma carga total e a carga total da casca externa é zero, sendo que ambas estão isoladas.
Determine a densidade de carga em cada superfície da camada;
Encontre as expressões para o potencial elétrico em todo espaço: , , e . Suponha que no infinito;
Calcule a diferença de potencial entre os ponto e na camada esférica externa;
Ver solução completaQuestão 18
Uma distribuição continua de cargas é constituída por um anel de raio , com densidade linear de carga uniforme , e um anel fracionado concêntrico de raio e densidade linear de carga uniforme , ambos no plano e com o mesmo eixo .
O anel fracionado é constituído por quatro arcos de circunferências idênticos, e cada arco é separado do seguinte por um ângulo , conforme a figura abaixo.
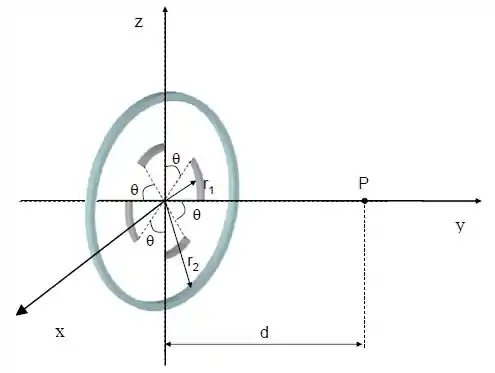
Calcule o potencial elétrico gerado pela distribuição de carga no ponto que se encontra sobre o eixo a uma distancia da origem.
Se o anel fracionado for girado de um ângulo arbitrário entorno do seu eixo, o resultado mudaria? Justifique as suas afirmações.
Qual deve ser o valor da razão para o potencial no ponto ser igual a zero?
Trace o gráfico de em função do ângulo . Descreva o andamento encontrado justificando as suas afirmações.
Ver solução completaQuestão 19
Considere um anel não-condutor situado no plano de raio interno e raio externo com uma densidade superficial de carga uniforme , como pode ser observado na figura.
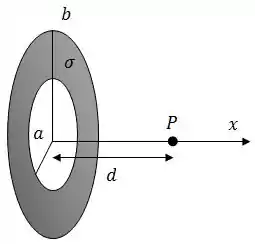
Calcule o potencial elétrico gerado por esta distribuição no ponto , a uma distância sobre o eixo indicado na figura.
A partir do resultado do item , encontre o campo elétrico (modulo, direção e sentido) no ponto .
Calcule o trabalho realizado para trazer uma carga puntiforme do infinito até o ponto .
Ver solução completaQuestão 20
Denomina-se coroa anular um disco fino de raio externo com buraco circular concêntrico de raio interno como mostrado em figura. Uma coroa anular possui uma densidade superficial de carga sobre sua superfície (.
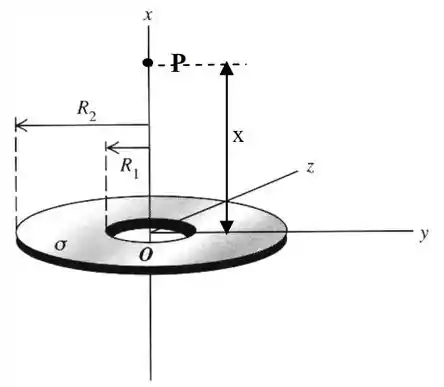
Determine a carga total sobre a coroa anular.
A coroa anular está sobre um plano com seu centro na origem. Para um ponto arbitrário sobre o eixo (eixo de simetria da coroa anular), determine o potencial (Sugestão: calcule o potencial devido a um anel de raio e espessura compreendido entre e e depois extenda o resultado para a coroa anular.)
Calcule agora o campo elétrico (módulo, direção e sentido) no ponto .
Uma carga positiva puntiforme é inicialmente colocada a repouso no ponto e a seguir liberada. Qual será a energia cinética desta carga quando passa no centro da coroa anular? (Considere neste item ; ; )
Ver solução completaQuestão 21
Considere um semi-anel circular, fino, de raio , situado no plano , conforme mostra a figura. Suponha que a densidade linear de carga de tal semi-anel seja dada por
onde é o tradicional ângulo polar, medido no sentido anti-horário, a partir do eixo .
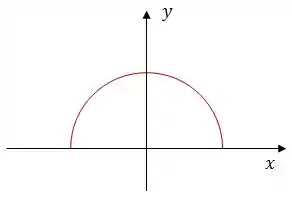
Qual é a carga elétrica total, , do semi-anel?
Calcule o campo elétrico na origem.
Calcule o potencial eletrostático em um ponto qualquer do eixo , com cota (Sabendo-se que o potencial no infinito é nulo).
Que componente(s) do campo elétrico, no mesmo ponto mencionado no item , pode(m) ser deduzida(s) a partir do resultado obtido no item anterior? Justifique e deduza-a(s).
Ver solução completaQuestão 22
A figura abaixo mostra duas distribuições de carga isoladas. Na esquerda, um anel circular fino, isolante, de raio , encontra-se uniformemente carregado e possui uma carga total . Na direita, uma coroa circular fina, isolante, de raio interno e raio externo encontra-se uniformemente carregada com uma densidade superficial de carga . Em ambas as situações, considere que o potencial elétrico produzido por cada uma das distribuições é nulo em um ponto infinitamente afastado delas. Considere ainda que o eixo é perpendicular ao plano definido por cada distribuição e passa pelo centro delas.
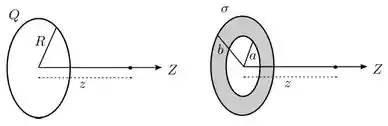
(a) Determine o potencial elétrico produzido pelo anel em um ponto sobre o eixo, localizado a uma distância do centro do anel.
(b) Determine o potencial elétrico produzido pela coroa em um ponto sobre o eixo , localizado a uma distância do centro da coroa.
Sugestão: Divida a coroa em aneis infinitesimais concêntricos e utilize o resultado do item anterior.
(c) Obtenha uma expressão assintótica para o potencial encontrado no item (b) no limite em que o ponto está muito distante do centro da coroa, de forma que. Interprete o resultado.
Ver solução completaQuestão 23
Um fio retilíneo fino, de comprimento , está postado ao longo do eixo cartesiano , com seu centro na origem desse. A densidade linear de carga de tal fio é dada por:
Onde .
- Calcule o potencial eletrostático para um ponto arbitrário no eixo cartesiano , com ordenada . Faça, como usual, o potencial igual a zero no infinito [Sugestão: lembre-se que, para temos simplesmente ao passo que para temos ].
- Calcule, agora, a componente do vetor campo elétrico em tal ponto;
- Determine, por fim, a carga total de tal fio.
Questão 24
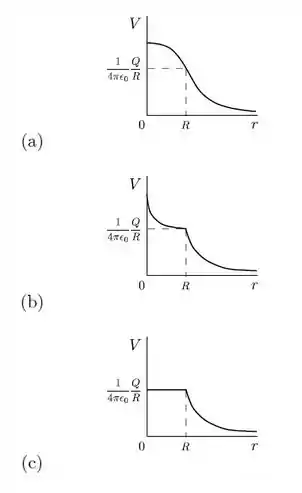
Qual dos gráficos abaixo melhor representa o potencial eletrostático de uma esfera de raio e carga uniformemente distribuída em todo o seu interior, supondo o potencial zero no infinito?
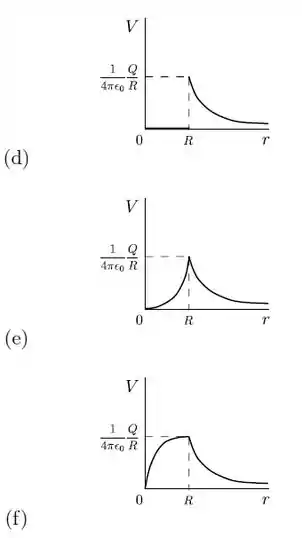
Questão 25
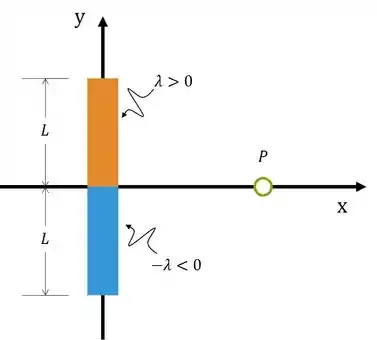
Um fio de comprimento foi carregado de modo a dotar a metade superior com densidade linear de carga e a metade inferior com densidade linear de carga , onde é uma constante positiva.
- Determine o campo elétrico (módulo, direção e sentido) num ponto situado a uma distância do fio, na direção perpendicular a partir de seu ponto médio.
- Obtenha o potencial elétrico no ponto supracitado.
- Mesmo para grandes distâncias () o campo elétrico não é exatamente nulo. Qual é o comportamento do campo elétrico, como função de , nessa aproximação? Interprete seu resultado
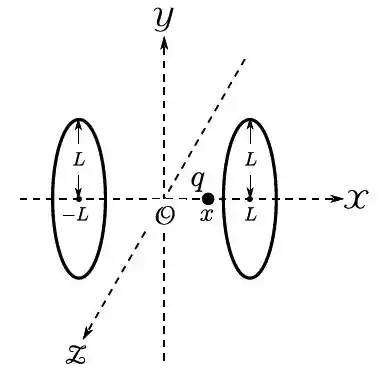
Questão 26
Dois anéis circulares, de mesmo raio , perpendiculares ao eixo , tem seus centros em e . Ambos possuem a mesma carga total , uniformemente distribuída.
- Determine o potencial elétrico devido aos anéis, em um ponto genérico do eixo , com abscissa , tomando tal potencial como zero no infinito ().
- Usando o potencial do item (a), determine o campo elétrico devido aos anéis, no mesmo ponto supracitado.
- Considere agora uma partícula de carga , ainda no mesmo ponto supracitado. Determine a energia potencial associada à interação dessa partícula com o campo elétrico produzido pelos anéis!
Questão 27
Dois fios retilíneos de mesmo comprimento , separados por uma distância , estão uniformemente carregados com densidades lineares de carga e .
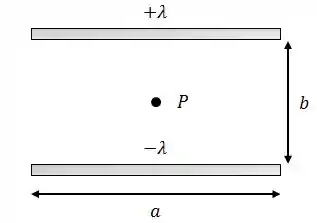
- Calcule o campo elétrico no ponto , centro do retângulo de lados e ;
- Calcule o potencial elétrico nesse ponto, supondo que no infinito;
- Se uma carga de prova for colocada no ponto , qual é a força instantânea que age sobre ela?
Questão 28
Uma carga puntiforme está no centro de uma fina casca esférica condutora de raio , carregada com carga .
Justaposta a esta casca encontra-se uma camada de material dielétrico de constante dielétrica , tendo raio externo .
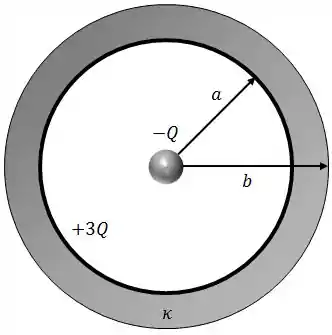
Encontra o vetor campo elétrico para , , ;
Calcule a ddp ;
Tomando , calcule para .
Ver solução completaQuestão 29
Uma carga total está distribuída por duas esferas metálicas de raios e , que estão ligadas por um fio condutor muito longo de comprimento , sendo e .
Determine:
- A carga sobre cada esfera;
- O potencial das esferas em função de ;
- A força de tração do fio;
Questão 30
A figura mostra uma barra fina de plástico de comprimento , sobre o eixo , carregada com densidade uniforme de carga .
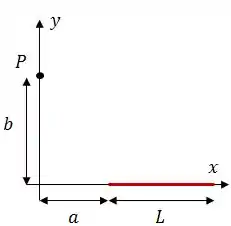
Com no infinito:
Calcule o potencial elétrico no ponto sobre o eixo ;
Determine, a partir do potencial, a componente do campo elétrico em ;
Por que a componente do campo elétrico neste ponto não pode ser calculada usando o resultado do item ?
Dado:
Ver solução completaQuestão 31
Há dois anéis com centros no mesmo eixo a uma distância um do outro e de raio também .
O anel possui carga uniformemente distribuída, e o anel 2 possui carga uniformemente distribuída.
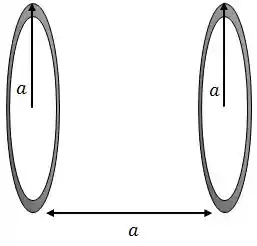
- Qual o potencial elétrico no centro de cada um dos anéis?
- Se colocarmos uma carga no centro do anel 1, qual o trabalho necessário que um agente externo deve realizar para leva-la até o centro do anel 2? (O sinal tem significado físico!)
Questão 32
Uma esfera de raio tem densidade volumétrica de carga uniforme. Determine a expressão para o campo elétrico em um ponto arbitrário do espaço em função da sua distância ao centro da esfera e use este resultado para determinar a expressão do potencial elétrico em função de na mesma região do espaço.
Ver solução completaQuestão 33
O eixo de um cilindro condutor de de raio dista do plano conforme a figura. O cilindro é infinito na direção perpendicular ao plano da figura e todo o semiespaço é preenchido com um material condutor.
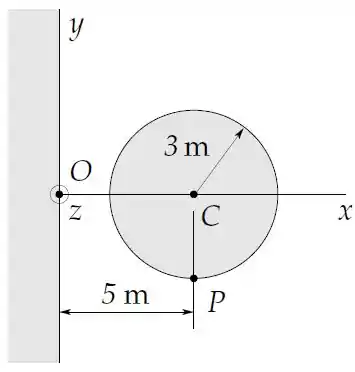
O potencial eletrostático num ponto de coordenadas no espaço fora dos condutores é dado por
onde e são em metros.
Determine o potencial no ponto do eixo do cilindro condutor .
Determine o vetor campo elétrico em todo o espaço, inclusive no interior dos condutores.
Determine a densidade superficial de carga no ponto do plano , e no ponto do cilindro. Adote .
Ver solução completaQuestão 34
Considere um bastão de comprimento e carregado com densidade linear uniforme de carga disposto conforme a figura.
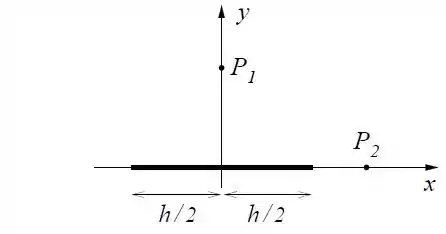
- Calcule o vetor campo elétrico no ponto de coordenadas , para .
- Calcule o potencial elétrico no ponto de coordenadas . Para .
- A partir do potencial calcule a componente do campo elétrico no ponto de coordenadas , para .
Questão 35
Dois anéis finos concêntricos de raios e , encontram-se no plano . O centro dos anéis coincide com a origem do sistema de coordenadas, conforme a figura. O anel de raio possui carga total e o anel de raio possui carga total , ambas uniformemente distribuídas.
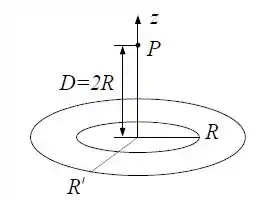
Calcule o potencial produzido por cada anel sobre o eixo .
Determine qual deve ser a carga no anel de raio para que ele produza no ponto do eixo , que está a uma distância da origem, o mesmo potencial eletrostático do anel de raio .
A partir do potencial, calcule o vetor campo elétrico em , em termos de e .
Ver solução completaQuestão 36
Um bastão de comprimento , eletrizado com densidade de carga não uniforme está disposto ao longo do eixo .
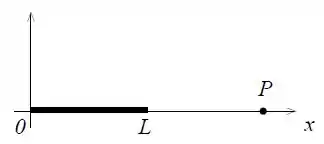
Determine o potencial eletrostático devido ao bastão para um ponto sobre o eixo com coordenada . Adote o potencial nulo no infinito.
Determine o vetor força de interação eletrostática sobre uma carga pontual em .
Ver solução completaQuestão 37
Um fio finito muito longo de comprimento e carregado com uma carga está no eixo de um cano cilíndrico condutor descarregado de raio interno , raio externo e mesmo comprimento .
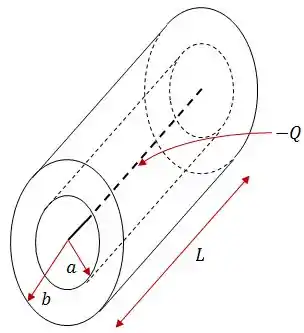
Que cargas aparecem nas superfícies interna e externa do cano?
Utilize a Lei de Gauss para calcular o vetor campo elétrico para , e ;
Calcule a diferença de potencial ;
Ver solução completaQuestão 38
Considere uma coroa circular com uma distribuição superficial de carga constante (estacionária e uniforme), onde . A coroa possui raio interno e raio externo e está localizada no plano , com o seu centro na origem, conforme ilustra a figura abaixo.
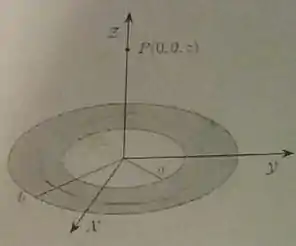
(a) Calcule o potencial eletroestático gerado por essa coroa circular no ponto , localizado no eixo , conforme ilustra a figura.
(b) Calcule o vetor campo elétrico gerado por essa coroa circular no ponto , localizado no eixo , conforme ilustra a figura.
Considere agora o limite em que o raio externo tende ao infinito, de forma que passamos a ter um plano infinito com um orifício circular de raio . A distribuição de carga contínua sendo uniforme, com densidade superficial . Para essa nova configuração, responda às perguntas a seguir.
(c) Considere que uma partícula de teste, de massa e carga , onde , tenha sido abandonada do repouso no ponto , Calcule a posição de equilíbrio da partícula no eixo . Adote a aceleração da gravidade como .
(d) Calcule a variação da energia potencial eletroestática da partícula de carga , a partir do momento em que ela foi abandonada do ponto , até passar pela origem do sistema de coordenadas.
Ver solução completaQuestão 39
Considere um arame fino de comprimento , disposto ao longo do eixo simetricamente em torno do ponto . Neste arame há uma densidade linear de carga , onde é uma constante. Encontre a expressão para o potencial eletroestático num ponto genérico do plano (ou seja, plano , a uma distância do arame (supondo que, no infinito, o potencial se anule).
a)
b)
c)
d)
e) 0
Ver solução completaQuestão 40
Uma meia coroa circular isolante de espessura desprezível (veja a figura abaixo), com raio interno e raio externo , está carregada com uma carga total Q > 0. A densidade superficial de carga não é uniforme e vale , onde é uma constante positiva e é a distância do centro da coroa até qualquer ponto sobre ela.
Considere o potencial nulo no infinito.
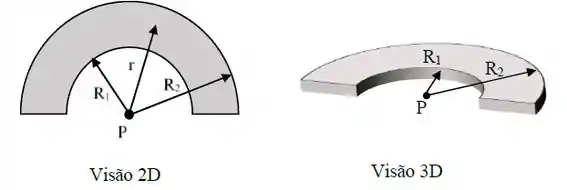
a) Determine a expressão para a carga total Q na meia coroa em função dee.
b)Obtenha uma expressão para o potencial elétrico no ponto P situado no centro da meia coroa, em função de e.
c) Considere agora uma aproximação em que o raio interno se iguale ao raio externo (a meia coroa circular se transforma em um meio anel). Neste caso, vamos considerar uma densidade linear de carga uniforme e igual a . Calcule, nesta condição:
i) a carga total Q do meio anel;
ii) a expressão para o potencial elétrico no ponto P no centro do anel.
d)Calcule o trabalho que deve ser realizado por um agente externo para transportar uma carga do infinito até o ponto P.
Ver solução completaQuestão 41
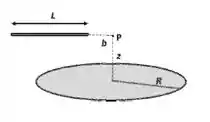
O ponto está sobre o eixo do disco à distância de seu centro e, simultaneamente, sobre o eixo da barra, à distância de sua extremidade mais próxima. (Nos itens () e () você pode escolher sistemas de coordenadas diferentes e convenientes a cada caso.)
- Considerando apenas o disco, calcule o potencial elétrico em .
- Considerando apenas a barra, calcule o potencial elétrico em .
- Calcule a velocidade da partícula ao passar por .
Considere, agora, outros dois pontos e do espaço (não mostrados na figura). No ponto , os potenciais do disco e da barra, separadamente, possuem valor e . No ponto , os potenciais valem e . Na presença tanto do disco quanto da barra, uma partícula de massa e carga é abandonada a partir do repouso do ponto e, sob ação exclusivamente das forças elétricas, passa pelo ponto .
Questão 42
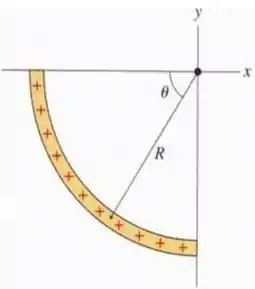
Uma barra isolante uniformemente carregada com carga é dobrada em forma de um quarto de círculo como mostra a figura.
![]()
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 43
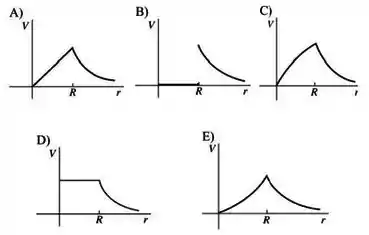
Uma esfera condutora de raio carregada com um excesso de carga positiva está muito longe de quaisquer outras cargas. Qual dos gráficos ilustra o potencial elétrico devido à esfera carregada em função da distância ao centro da esfera.
Considere a origem do potencial em
Questão 45
Uma esfera uniformemente carregada em todo seu volume com uma carga tem um raio de . Quanto vale o potencial na superfície da esfera e no seu centro com relação ao infinito.
e ;
e zero;
e zero;
e ;
e ;
Ver solução completaQuestão 46
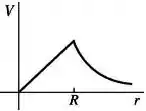
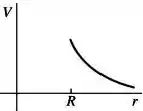
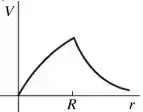
Uma esfera condutora de raio possui um excesso de carga positiva e está muito longe de quaisquer outras cargas. Qual dos seguintes gráficos ilustra melhor o potencial (em relação ao infinito) produzido por esta esfera em função da distância a partir do centro da esfera?
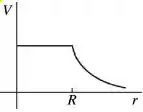
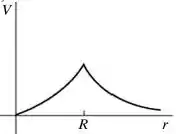
Questão 47
Dois anéis finos concêntricos de raios e , encontram-se no plano . O centro dos anéis coincide com a origem do sistema de coordenadas, conforme a figura. O anel de raio possui carga total e o anel de raio possui carga total , ambas uniformemente distribuídas.
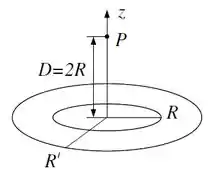
(a) Calcule o potencial produzido por cada anel ao longo do eixo , como função de .
(b) A partir do potencial, calcule a componente do campo elétrico em , em termos de e . Quanto valem as componentes e do campo elétrico? Justifique.
(c) Determine qual deve ser a carga no anel de raio para que ele produza no ponto do eixo , que está a uma distância da origem, o mesmo potencial eletrostático do anel de raio .
Ver solução completaQuestão 48
. Um plano infinito é posicionado sobre o plano de um sistema de coordenadas. Ele encontra-se carregado com uma densidade superficial de carga constante .
Sabendo que o campo elétrico produzido pelo plano em um ponto qualquer do espaço tem a forma , utilize a lei de Gauss para determinar , considerando as regiões e .
Determine o potencial elétrico produzido pelo plano no ponto , considerando as mesmas regiões acima. Considere que o potencial é nulo sobre o próprio plano.
Ver solução completaQuestão 49
Um anel circular de raio está carregado com uma densidade de carga positiva e não uniforme, , onde . Determine:
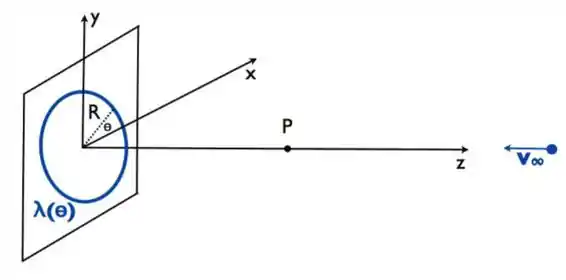
a carga total no anel.
o potencial eletrostático, , num ponto do eixo de simetria do anel, localizado a uma distância do seu centro (sabendo-se que no infinito).
a expressão do campo elétrico, , no ponto , a partir de .
o módulo da velocidade inicial, , que um próton, de massa e carga , deve ter, em , para que este chegue ao repouso no centro do anel, em
Ver solução completaQuestão 50
Um anel circular isolante está posicionado sobre o plano de um sistema de coordenadas, de forma que seu centro coincida com a origem. A situação é mostrada na figura abaixo.
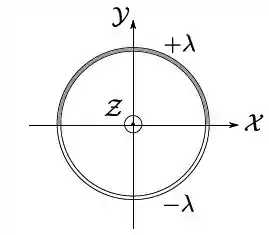
O anel possui uma densidade linear de carga constante em sua metade superior e em sua metade inferior . Utilizando o sistema de eixos da figura e tomando o potencial eletrostático como nulo no infinito, considere as afirmativas abaixo:
O potencial eletrostático é nulo em qualquer ponto sobre o eixo OZ.
O campo elétrico aponta no sentido negativo do eixo em qualquer ponto sobre o eixo .
O trabalho realizado pela força elétrica ao trazer uma partícula de carga do infinito ao centro do anel é positivo.
São VERDADEIRAS as afirmativas:
e
e
e
, e
Nenhuma delas.
Ver solução completaQuestão 51
Uma barra unidimensional de comprimento com densidade linear de carga está sobre o eixo . A extremidade esquerda da barra está localizada em . Quanto vale a intensidade do campo elétrico, na unidade gerado por esta distribuição de cargas no ponto (localizado no eixo ) a uma distância da extremidade direita da barra? Se necessário use .
Ver solução completaQuestão 52
Q - Dado um potencial eletrostático expresso em coordenadas cartesianas, o campo elétrico associado é:
Ver solução completaQuestão 53
A figura 3 ilustra uma barra não-condutora unidimensional, de comprimento , posicionada ao longo do eixo .
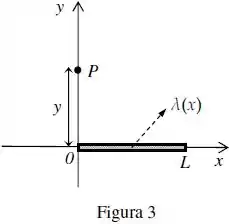
A barra tem uma densidade linear de carga variável , onde é uma constante positiva e . O ponto indicado na figura 3 está localizado ao longo do eixo vertical, a uma distância da origem do sistema de coordenadas.
Admita que o potencial elétrico é nulo no infinito. Para tais circunstâncias:
Calcule o potencial elétrico no ponto .
Calcule a componente do campo elétrico no ponto .
A componente do campo elétrico no ponto pode ser calculada usando o resultado do item (a)? Justifique sua resposta.
Ver solução completaQuestão 54
Uma esfera sólida metálica de raio e uma casca esférica bidimensional, de raio são concêntricas e estão, cada uma, em equilíbrio eletrostático (sem contato). Na esfera interna, existe uma carga , qao passo que, na casca externa, existe uma carga . Qual das afirmativas abaixo corresponde ao potencial eletrostático desse sistema nas regiões:
Considere o potencial como zero no infinito.
Questão 55
Uma esfera, de raio e carga total , possui uma densidade volumar (resultante) de carga estacionária, mas não uniforme, dada por:
Onde é uma constante e é a distância até o seu centro. Essa esfera está envolta por uma casca esférica condutora, concêntrica, de raio interno e raio externo , com carga total , em equilíbrio eletrostático.
- Expresse a constante como função de e de .
- Quais são as densidades superficiais de carga na casca esférica condutora?
- Determine o campo elétrico nas quatro regiões:
- Determine o potencial eletrostático nas quatro regiões supracitadas, tomando-o como zero no infinito.
Questão 56
A figura abaixo ilustra um anel fino não condutor de raio , com carga positiva uniformemente distribuída ao longo de sua circunferência.
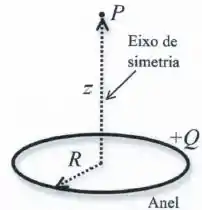
Considerando que o potencial elétrico é zero no infinito, calcule em um ponto que está localizado sobre o eixo de simetria do anel, a uma distância do seu centro.
A partir da expressão do potencial obtida em , calcule o valor da componente do campo elétrico na direção .
A expressão para obtida em permite calcular a componente do campo elétrico, mas não as componentes e . Por quê?
Uma partícula com carga elétrica e massa é lançada do infinito em direção ao anel, ao longo do seu eixo de simetria. Calcule a velocidade de lançamento mínima para que a partícula atravesse o plano do anel.
Ver solução completaQuestão 57
Uma barra isolante fina é posicionada sobre o eixo de um sistema de coordenadas, como mostrado na figura abaixo. O eixo é perpendicular à barra e a origem do sistema coincide com o seu ponto médio. A distribuição de cargas na barra é tal que sua metade à direita está uniformemente carregada com uma densidade linear de carga () e sua metade à esquerda está uniformemente carregada com uma densidade linear de carga . Sobre essa situação, considere as seguintes alternativas:
(I) Para todos os pontos sobre o eixo , o campo elétrico aponta no sentido negativo de .
(II) Para pontos sobre o eixo , é possível determinar a intensidade do campo elétrico conhecendo apenas o potencial elétrico sobre esses pontos.
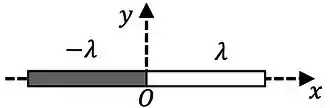
São corretas as alternativas:
(a) Apenas I
(b) Apenas II
(c) Nenhuma delas
(d) Todas elas
Ver solução completaQuestão 58
Um anel circular isolante de raio possui uma carga uniformemente distribuída sobre seu comprimento. Uma partícula de carga e massa encontra-se inicialmente em repouso sobre o eixo do anel, em um ponto muito afastado de seu centro. Desprezando a ação da gravidade, os módulos da velocidade e da aceleração dessa partícula quando ela passa pelo centro do anel valem, respectivamente:
(a) e
(b) e
(c) e
(d) e
(e) e
Ver solução completaQuestão 59
Duas esferas condutoras, uma tendo o dobro do diâmetro da outra, estão separadas a uma
distância muito maior que seus diâmetros. A esfera menor (1) tem carga e a esfera maior (2) está descarregada.
Se as esferas forem conectadas por um fio condutor, então será correto afirmar que as cargas da esfera menor (1) e da esfera maior (2) serão, respectivamente:
- e
- e
- e
- e
- e
Questão 60
Seja uma casca esférica não condutora de raio interno e raio externo , veja a figura. A carga total na casca é e está uniformemente distribuída no seu volume. Considere no infinito.
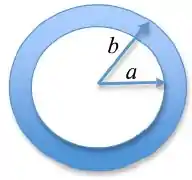
Calcule o módulo do campo elétrico e o potencial elétrico para , onde é a distância de um ponto no espaço ao centro da casca.
Calcule a densidade volumétrica de carga na casca.
Calcule o módulo do campo elétrico para e para .
Calcule o potencial elétrico para e para .
Ver solução completaQuestão 61
Uma barra semicircular de comprimento é composta de três segmentos não-condutores de mesmo comprimento. O segmento do meio é eletricamente neutro e os segmentos das extremidades têm uma carga negativa uniformemente distribuída.
Determine:
O vetor campo elétrico no centro do arco semicircular;
O potencial elétrico total nesse ponto;
A máxima velocidade que um elétron pode adquirir quando este é solto a partir do repouso no centro da barra semicircular.
Ver solução completaQuestão 62
Um anel circular de raio e uma casca esférica de raios e têm centro comum, situado na origem de um sistema de coordenadas.
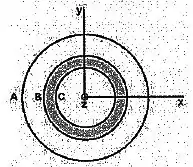
Uma carga total está uniformemente distribuída no anel. Uma carga total está uniformemente distribuída na casca esférica. Sabe-se que e que o anel está contido no plano , conforme mostra o corte da configuração representado na figura acima.
Determine o vetor campo elétrico devido à casca esférica em um ponto arbitrário do eixo tal que .
A partir do resultado do item , determine o potencial elétrico devido à casca esférica no mesmo ponto.
Determine o potencial elétrico devido ao anel no mesmo ponto.
A partir do resultado do item , determine o vetor campo elétrico devido ao anel no mesmo ponto.
Indique, justificando, o sinal do potencial elétrico e o sentido do vetor campo elétrico devidos à configuração total (anel e casca) no ponto arbitrário do eixo tal que .
Ver solução completaQuestão 63
Um cilindro muito longo maciço condutor, de raio e densidade de carga por unidade de comprimento , é concêntrico a uma camada cilíndrica condutora carregada com a mesma carga total do cilindro, em módulo, e sinal oposto.
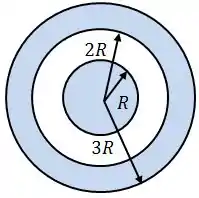
Essa camada tem raio interno e raio externo , como mostra a figura.
Determine o campo elétrico para as regiões e .
Determine a diferença de potencial entre os pontos e , ou seja, .
Ver solução completaQuestão 64
Considere a casca esférica isolante representada na figura abaixo.
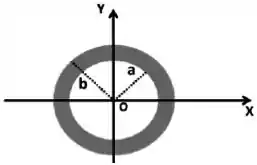
O centro da casca esférica coincide com as origens dos eixos . O raio interno da casca é , aquele externo . A densidade volumétrica de carga NÃO é uniforme e tem a seguinte expressão:
Calcule as unidades de medida da constante .
Calcule o potencial elétrico na origem dos eixos.
Calcule o campo elétrico na origem dos eixos, SEM utilizar a Lei de Gauss.
Suponha agora que a carga liquida da casca esférica se conserve, mas que o material isolante seja trocado por um material condutor. Seja o valor da carga líquida (conhecido).
Calcule, em função de , o valor das densidades superficiais de cargas e (interna e externa) da casca esférica.
O potencial elétrico na origem dos eixos muda de valor em comparação ao valor calculado no item ? Se não mudar, justifique porquê. Se mudar, calcule o novo valor em função de , usando o método que preferir.
Ver solução completaQuestão 65
Uma coroa circular está uniformemente carregada com densidade superficial de carga , onde . A coroa possui raio interno , raio externo e está localizada no plano com o seu centro na origem, como mostrado na figura abaixo.
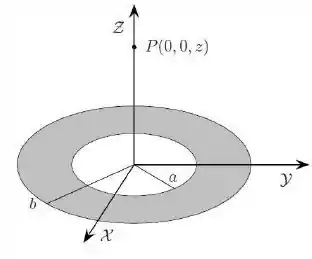
Determine a carga total da coroa.
Determine a expressão para o potencial eletrostático gerado por essa coroa circular no ponto , localizado no semieixo positivo .
Determine o campo elétrico (módulo, direção e sentido) gerado por essa coroa circular no ponto , localizado no semieixo positivo .
Formulário
Ver solução completaQuestão 66
Considere um elemento de carga de comprimento situado em uma posição qualquer da linha, veja a ilustração. Escreva o potencial que este elemento produz em , com .
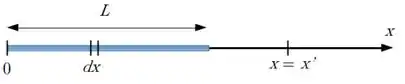
(a) Determine o potencial elétrico produzido por toda a linha de carga em , com .
(b) Use o resultado do item (b) para calcular o campo elétrico em .
(c) Suponha que uma carga puntiforme esteja em . Determine o trabalho mínimo que um agente externo deve realizar para levar a carga para .
Ver solução completaQuestão 67
Uma barra fina e isolante de comprimento é posicionada sobre o eixo de um sistema de coordenadas com seu centro sobre a origem, como mostrado na figura abaixo. Ela possui uma densidade linear de carga estacionária e não-uniforme dada por , onde é uma constante positiva. Considere que o potencial eletrostático é nulo no infinito.

(a) Determine o potencial eletrostático em um ponto sobre um eixo , a uma distância da origem.
(b) Determine o campo eletrostático (módulo, direção e sentido) no mesmo ponto .
(c) Obtenha uma expressão assintótica para o resultado do item (a) no limite . Interprete o resultado
Ver solução completaQuestão 68
Considere um plano isolante infinito situado em com uma densidade superficial de carga , como indicado na Figura 1. Tomando como o ponto de referência para o potencial, encontre o potencial nas seguintes regiões:
(a) .
(b) .
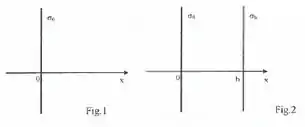
Suponha que no ponto seja colocado um plano isolante infinito com uma densidade superficial de carga (Figura 2).
(c) Nesta nova situação, encontre o potencial na região entre as duas placas.
(d) Considere agora que uma partícula de massa e carga é colocada em repouso em . Em que direção a partícula se move? Encontre a velocidade final dela ao atingir a placa.
Ver solução completaQuestão 69
A figura abaixo representa um disco não condutor com um furo central com raios e . O disco está carregado com densidade superficial de carga .
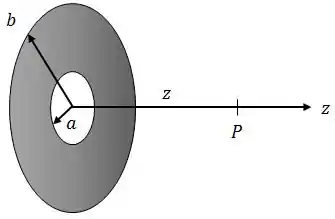
- Calcule o potencial elétrico no ponto , a uma distância do disco situado sobre o seu eixo central;
- A partir do potencial encontrado no item , calcule o vetor campo elétrico no ponto ;
- Fazendo simultaneamente e tendendo para infinito , que vetor campo elétrico resulta?
Questão 70
Na figura abaixo temos uma esfera não condutora de raio carregada com uma carga distribuída uniformemente em todo o seu volume (densidade volumétrica de cargas constante e igual a ).

Calcular:
O potencial para e ;
Qual é a diferença de potencial entre um ponto da superfície da esfera, e o potencial no centro da mesma ?
Obter a componente do campo elétrico para e ;
Ver solução completaQuestão 71
Uma placa plana isolante, de espessura desprezível, infinita, possui densidade superficial de carga constante. Um elétron (carga ), inicialmente em repouso, é deslocado lentamente por um agente externo de uma posição inicial, cuja distância à placa é até uma posição final, cuja distância à placa é , e deixado em repouso. Qual é o trabalho realizado pelo agente externo sobre o elétron nesse percurso?
Questão 72
Um anel circular fino de raio está uniformemente carregado com uma densidade linear de carga . Uma barra fina, de comprimento igual ao raio do anel e uniformemente carregada com a mesma densidade é posicionada inicialmente ao longo do eixo , que é perpendicular ao plano do anel e passa por seu centro, como mostrado na Figura à esquerda abaixo. A barra é posicionada de forma que uma de suas extremidades coincida com o centro do anel, como indicado na figura.
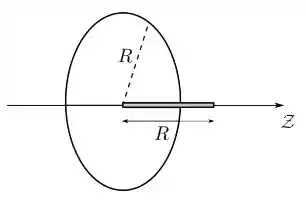
- Determine o potencial eletrostático produzido apenas pelo anel em um ponto sobre o eixo , localizado a uma distância do centro do anel. Considere que o potencial é nulo no infinito.
- Determine o campo eletrostático (módulo, direção e sentido) produzido apenas pelo anel no mesmo ponto .
- Determine a energia potencial eletrostática associada à interação entre o anel e a barra. Considere que a energia é nula quando o anel e a barra estão infinitamente afastados um do outro. Sugestão: Divida a barra em elementos de carga infinitesimais e considere a contribuição da interação entre este elemento e o anel para a energia total.
- Determine o trabalho realizado pela força eletrostática ao fazermos a barra atravessar completamente o anel, colocando-a em uma nova configuração onde sua extremidade oposta coincide com o centro do anel, como mostrado na figura abaixo. Justifique sua resposta.
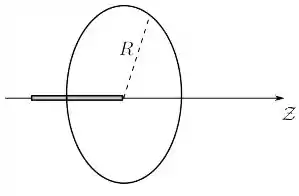
Formulário:
Ver solução completaQuestão 73
Duas esferas metálicas carregadas, de raios distintos, estão conectadas por um fio condutor muito fino. Sabendo que e representam os módulos do campo elétrico na superfície das 1, 2, e e as densidades superficiais, assinale a opção que descreve as relações entre os valores de e de no equilíbrio eletrostático (quando os potenciais na superfície são iguais).
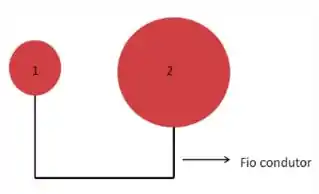
Questão 74
Um capacitor esférico é formado por dois condutores em equilíbrio eletrostático. O condutor interno possui formato esférico, de raio , e está carregado com uma carga total . O segundo condutor, de raio interno e raio externo , está carregado com uma carga total .
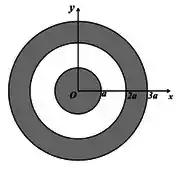
(a) Determine o vetor campo elétrico em todo o espaço e indique como as cargas elétricas estão distribuídas em cada um dos condutores.
(b) Determine o potencial elétrico em todo o espaço. Assuma que o potencial é zero no infinito.
(c) Calcule a capacitância do capacitor.
Ver solução completaQuestão 75
A figura abaixo ilustra um disco circular não-condutor oco, de raio interno , raio externo e centro , que tem uma densidade superficial de carga constante . O ponto está localizado a uma distância do ponto e o segmento define o eixo de simetria que passa pelo centro do disco oco, sendo perpendicular ao plano do disco. Considere que o potencial elétrico é zero no infinito, ou seja, . Nesta situação, calcule:
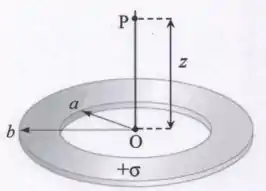
- O potencial elétrico no ponto .
- O vetor campo elétrico (módulo, direção e sentido) no ponto .
- A energia potencial elétrica adquirida por uma carga pontual que seja colocada no ponto .
Questão 76
Um semianel fino, de raio é posicionado sobre os dois primeiros quadrantes do plano de um sistema de coordenadas com seu centro sobre a origem, como indicado na figura abaixo. Ele está carregado com uma densidade linear de carga não-uniforme dada por , onde é uma constante positiva e é o ângulo polar, medido a partir do eixo .
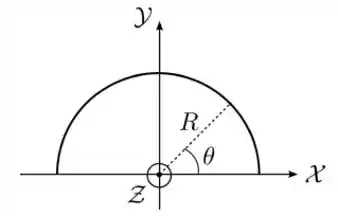
- Determine a carga total contida no semianel.
- Determine o potencial elétrico produzido pelo semianel em seu centro, considerando que o potencial é nulo em pontos infinitamente afastados do centro.
- Determine o campo elétrico (módulo, direção e sentido) produzido pelo semianel no mesmo ponto.
Questão 77
Considere um plano infinito , uniformemente carregado, coincidente com o plano de um dado sistema de coordenadas. Sobre esse sistema, considere as afirmativas abaixo:
- Pode-se tomar o potencial elétrico como nulo sobre todos os pontos do plano .
- Qualquer plano paralelo à é uma superfície equipotencial.
- A diferença de potencial elétrico entre os pontos de coordenadas e é nula.
São VERDADEIRAS as seguintes afirmativas:
- e
- e
- e
- e
- Nenhuma delas.
Questão 78
Considere uma esfera , de raio , uniformemente carregada com densidade volumétrica de carga positiva. Considere também três pontos no espaço, , e , onde os potenciais elétricos valem , e , respectivamente. Se está no interior da esfera, sobre sua superfície, e em seu exterior, temos, necessariamente,
Questão 79
Uma esfera condutora isolada está carregada com uma carga total negativa e encontra-se em equilíbrio eletrostático. Sejam , e pontos localizados no interior da esfera, na superfície da esfera e no exterior da esfera, respectivamente. Se os potenciais elétricos nestes pontos valem , e , podemos afirmar que:
Questão 80
Um cilindro condutor maciço, infinito, de seção transversal circular de raio possui uma densidade superficial de carga constante e positiva. Ele se encontra em equilíbrio eletrostático.
- Determine o vetor campo elétrico produzido pelo cilindro em um ponto a uma distância de seu eixo. Considere os casos dentro e fora do cilindro.
- Determine o potencial elétrico produzido pelo cilindro no mesmo ponto. Considere que o potencial vale sobre a superfície do cilindro.
Questão 81
Campo elétrico pode ser entendido de forma qualitativa como sendo a influência do campo da carga elétrica, que pode assumir diversas configurações. Seja um campo elétrico um, considerando o exposto, calcule a distancia entre dois pontos A e B em um campo elétrico uniforme de linhas paralelas e de intensidade igual a e d.d.p igual .
Ver solução completaQuestão 82
Uma barra isolante fina de comprimento é posicionada sobre o eixo de um sistema de coordenadas, como mostrado na figura abaixo. Suas extremidades estão nos pontos e . Ela encontra-se carregada com uma densidade linear de carga estacionária, mas não-uniforme dada por , onde e uma constante positiva.
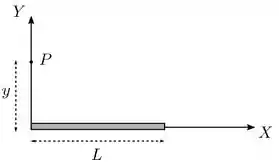
(a) Determine a carga total contida na barra.
(b) Determine o potencial elétrico produzido pela barra em um ponto sobre o eixo , localizado a uma distância acima da extremidade esquerda da barra. Considere que o potencial é nulo em um ponto infinitamente afastado da barra.
(c) A componente do campo elétrico no ponto pode ser obtida a partir do potencial obtido no item anterior? Justifique.
Ver solução completaQuestão 83
Considere um cilindro infinito com seção transversal circular de raio . Ele encontra-se carregado com uma densidade volumétrica de carga constante e negativa. Sejam , e pontos localizados no interior do cilindro, sobre a superfície do cilindro e fora do cilindro, respectivamente. O potencial eletrostático produzido pelo cilindro nestes pontos vale , e , respectivamente. Nessa situação, podemos afirmar que:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
Ver solução completaQuestão 84
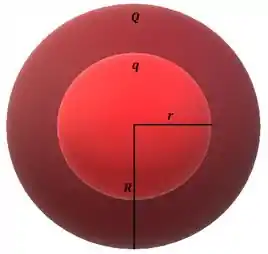
Entre as duas cascas esféricas delgadas condutoras concêntricas da figura não há nenhum contato elétrico. A casca interna possui raio e carga e a casca externa possui raio e carga . Considerando o referencial para potenciais nulos no infinito, sabe-se que o potencial na casca maior vale e na casca menor vale .
d) Calcule em função de , , , e da constante de Coulomb .
Questão 85
8 - Um grão de poeira tem a forma de uma esfera de raio igual a . Ele possui uma carga negativa uniformemente distribuída sobre seu volume, de forma que o potencial elétrico em sua superfície vale . Considerando que o potencial é nulo em um ponto infinitamente afastado do grão, podemos afirmar que a carga total do grão vale:
Questão 86
Uma barra isolante fina de comprimento 2L é posicionada sobre o eixo X de um sistema de coordenadas com seu ponto médio sobre a origem, como mostrado na figura abaixo. A porção possui uma densidade linear de carga constante e a porção possui uma densidade linear . Considere que o potencial elétrico produzido pela barra é nulo em um ponto infinitamente afastado dela.

(a) Determine o potencial elétrico produzido pela barra em um ponto P sobre o eixo X, localizado a uma distancia da origem.
(b) Determine uma expressão assintótica para o resultado encontrado no item anterior no limite . Interprete esse resultado.
Formulário: , com .
Ver solução completaQuestão 87
3 - O gráfico abaixo representa o potencial elétrico em função da posição . Qual das alternativas descreve corretamente a componente do campo elétrico ao longo do eixo ?
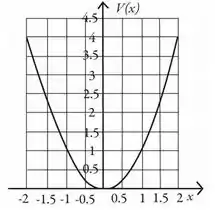
- é positiva de até
- é positiva de até e negativa de até
- é negativa de até e positiva de até
- é negativa de até
- é nula de até
Questão 88
2 - Se o campo elétrico aponta na direção no sentido de crescente e tem magnitude com uma constante, então o potencial elétrico no ponto vale (considere no ponto ):
Questão 89
A figura ilustra uma coroa circular disposta no plano , centrada na origem, de raio interno e raio externo . Sua carga está uniformemente distribuída e possui . Use ou .
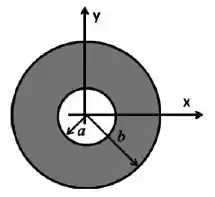
Considerando a referência para potenciais no infinito, encontre o valor do potencial elétrico num ponto qualquer do eixo , à distância da origem.
Calcule o potencial no ponto e o valor do trabalho realizado pela força eletrostática no deslocamento de uma carga teste desde até o ponto onde o potencial vale .
Suponha que o potencial gerado pela coroa circular no ponto tenha valor . Queremos anular o potencial em , e para isso dispomos de uma carga pontual de valor . Determine todos os pontos do espaço em que podemos posicionar a carga de modo a tornar nulo o potencial em .
Ver solução completaQuestão 90
Um fio de comprimento está carregado uniformemente com a densidade linear de carga . Determine uma expressão para o potencial elétrico em um ponto arbitrário do eixo , conforme mostra a Figura .
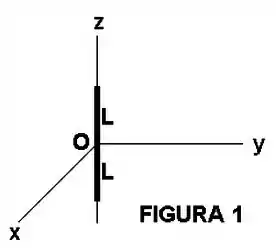
Adapte a solução do item para determinar o potencial elétrico devido a um fio quadrado de lado , carregado uniformemente com a densidade linear de carga , em um ponto de observação arbitrário do eixo , conforme mostra a Figura .
Sugestão: calcule a distância entre o ponto de observação e o ponto médio de um dos lados do quadrado.
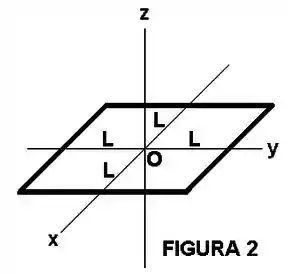
Determine o vetor campo elétrico devido ao fio quadrado no mesmo ponto de observação.
Ver solução completaQuestão 91
Seja um anel carregado com uma densidade linear de carga em uma de suas metades e na outra, sendo uma constante, e seja o eixo de simetria perpendicular ao plano do anel.
Sabendo que o potencial elétrico no infinito é igual a zero, qual a única afirmativa verdadeira?
e sobre o eixo
e sobre o eixo
e sobre o eixo
e no centro do anel
e no centro do anel
Ver solução completaQuestão 92
Duas esferas condutoras, de raios diferentes, têm ambas cargas . O que ocorre quando as duas esferas são ligadas por um fio condutor?
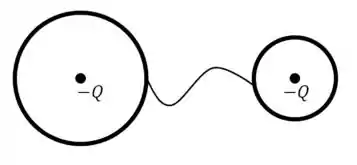
a) cargas negativas fluem da esfera menor para a maior até que os campos elétricos nas superfícies das duas esferas se igualem
b) cargas negativas fleum da esfera maior para a menor até que que os potenciais das duas esferas se igualem
c) não há fluxo de cargas entre as esferas
d) cargas negativas fluem da esfera menor para a maior até que os potenciais das duas esferas se igualem
e) cargas negativas fluem da esfera maior para a menor até que os campos elétricos nas superfícies das duas esferas se igualem
Ver solução completaQuestão 93
(Cap. 24 – Ex. 30)
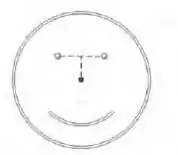
O rosto sorridente da Fig. Abaixo é formado por três elementos:
1: Uma barra fina com uma carga de e a forma de uma circunferência completa com 6,0 cm de raio;
2: Uma segunda barra fina com uma carga de e a forma de um arco de circunferência com de raio, concêntrico com o primeiro elemento, que subtende um ângulo de ;
3: Um dipolo elétrico cujo momento dipolar é perpendicular ao diâmetro da primeira barra que passa pelo ponto médio da segunda barra e cujo módulo é
Determine o potencial elétrico no centro da circunferência.
Questão 94
(Capítulo 24.9 – Exercício 27) Na Fig. abaixo, três barras finas de plástico têm a forma de quadrantes de circunferência com o mesmo centro de curvatura, situado na origem. As cargas uniformes das barras são = +30 nC, = +3,0 e = - 8,0. Determine o potencial elétrico na origem.
Questão 95
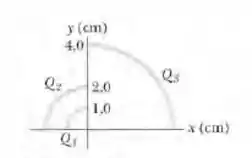
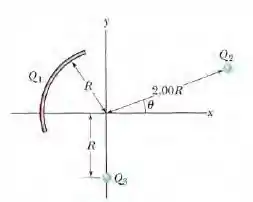
(Capítulo 24.9 – Exercício 29) Na Fig. abaixo, determine o potencial elétrico produzido na origem por um arco de circunferência de carga = +7,21 pC e duas partículas de cargas = 4,00 e = -2,00. O centro de curvatura do arco está na origem, o raio do arco é R = 2,00 m e o ângulo indicado é = 20,0º.
Questão 96
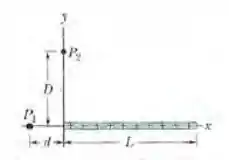
(Capítulo 24.9 – Exercício 28) A Fig. abaixo mostra uma barra fina de plástico que coincide com o eixo x. A barra tem um comprimento L = 12,0 cm e uma carga positiva uniforme Q = 56,1 fC uniformemente distribuída. Com V= 0 no infinito, determine o potencial elétrico no ponto do eixo x, a uma distância d = 2,50 cm de uma das extremidades da barra.
Questão 97
(Capítulo 24.10 – Exercício 35) O potencial elétrico no plano xy é dado por . Em termos dos vetores unitários, qual é o campo elétrico no ponto ?
Ver solução completaQuestão 98
(Capítulo 24.9 – Exercício 23)
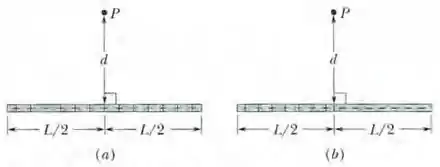
(a) A figura (a) mostra uma barra não condutora de comprimento e densidade linear de cargas positivas uniforme . Considere no infinito. Qual é o valor de no ponto situado a uma distância acima do ponto médio da barra?
(b) A figura (b) mostra uma barra idêntica à do item (a), exceto pelo fato de que a metade da direita agora está carregada negativamente; o valor absoluto da densidade linear de cargas continua a ser em toda a barra. Com no infinito, qual é o valor de no ponto ?
Questão 99
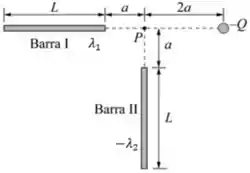
Q - A figura ao lado mostra duas barras isolantes de comprimento , que estão uniformemente carregadas com densidades lineares de cargas e , respectivamente, e uma carga puntiforme , situada a uma distância da Barra .
Determine o vetor campo elétrico, produzido no ponto , pelo conjunto (barras e carga).
Determine o potencial elétrico no ponto produzido pelo conjunto.
Supondo que , determine para que o campo elétrico faça um ângulo de com a horizontal.
Dica: Não se esqueça de explicitar qual é seu sistema de referências.
Questão 100
Duas esferas condutoras sólidas em equilíbrio eletrostático, de raios respectivos e , estão carregadas com cargas e respectivamente. Estas esferas estão colocadas a uma grande distância uma da outra de modo que o efeito da carga de uma esfera não interfere com a carga da outra.
d) Calcule o potencial eletrostático de cada esfera, assim como o campo elétrico na superfície de cada uma.
Conectando as duas esferas por um fio condutor perfeito muito fino atingimos um novo equilíbrio eletrostático.
e) Nesta nova situação, calcule as cargas de cada esfera.
Ver solução completaQuestão 101
Considere um plano infinito , uniformemente carregado. Sobre esse sistema, considere as afirmativas abaixo:
- O potencial eletrostático produzido por é constante sobre todos os pontos de um plano paralelo a .
- Como o campo eletrostático produzido por não depende da distância até o mesmo, o potencial também não dependerá.
- O potencial eletrostático produzido por necessariamente se anula em um ponto infinitamente afastado de .
São VERDADEIRAS as afirmativas:
- I
- II
- III
- I e II
- I e III
- II e III
- I, II e III
- Nenhuma delas.
Questão 102
Duas esferas condutoras, de raios diferentes, têm ambas cargas . O que ocorre quando as duas esferas são ligadas por um fio condutor?
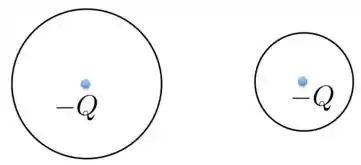
- as cargas negativas fluem da esfera menor para a esfera maior até que os campos elétricos nas superfícies das duas esferas se igualem;
- não há fluxo de cargas entre as esferas;
- as cargas negativas fluem da esfera maior para a esfera menor até que os potenciais das duas esferas se igualem;
- cargas negativas fluem da esfera menor para a esfera maior até que os potenciais das duas esferas se igualem;
- as cargas negativas fluem da esfera maior para a esfera menor até que os campos elétricos nas superfícies das duas esferas se igualem.
Questão 103
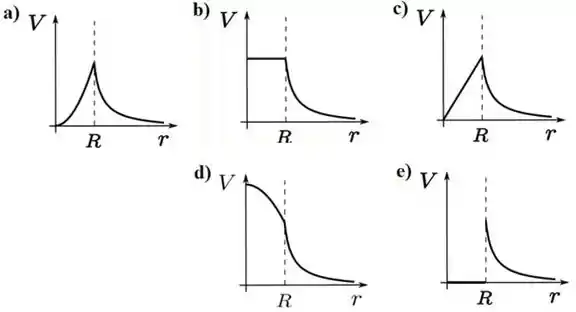
Considere uma esfera condutora maciça com densidade de carga constante (estacionária e uniforme) e raio . Qual das alternativas abaixo melhor representa o potencial elétrico em função da distância ao seu centro?
Questão 104
Uma certa distribuição estática de cargas produz um potencial eletrostático que depende apenas da distância até a origem de um sistema de coordenadas. O gráfico de é mostrado na figura abaixo, com quatro regiões destacadas. Sobre o campo eletrostático produzido por essa distribuição, , onde é o vetor unitário da direção radial, podemos afirmar que:
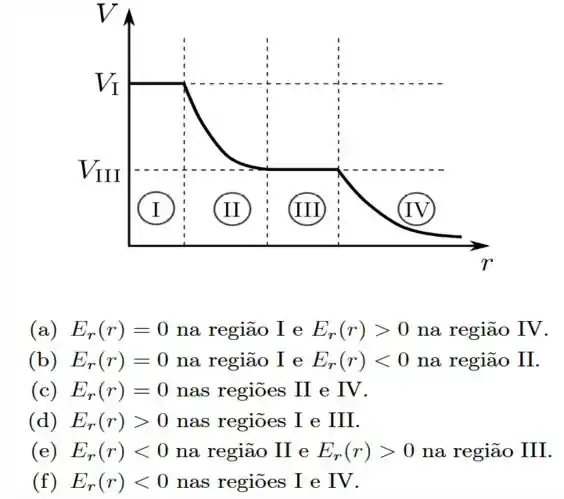
Questão 105
4 - Uma carga negativa, livre, tenderá a se mover
- do potencial elétrico mais alto para o potencial elétrico mais baixo.
- do potencial elétrico mais baixo para o potencial elétrico mais alto.
- em direção ao infinito.
- para longe do infinito.
- no sentido do campo elétrico.
Questão 106
Um fio retilíneo e infinito, carregado com uma densidade linear positiva e uniforme, , é colocado no interior de uma casca cilíndrica espessa, tambéminfinita,
Condutora e neutra, de raios interno, e externo, . Determine:
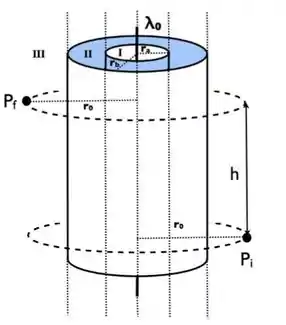
a carga contida num segmento de altura do fio,e as densidades superficiais de carga, e ,induzidas nas superfícies interna e externa do cilindro, respectivamente.
o campo elétrico, ,nas regiões
o potencial eletrostático, ,em todas as três regiões, apartir de,colocando o zero do potencial na superfície mais externado cilindro, de raio .
a.entreospontos e assinalados na figura (justifique sua resposta)
Ver solução completaQuestão 107
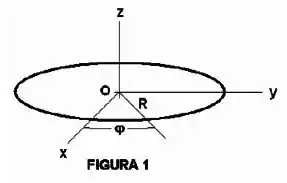
O anel de raio mostrado na Figura 1 tem a densidade linear de carga:
Determine uma expressão para o potencial elétrico em um ponto arbitrário do eixo (perpendicular ao plano do anel que contém a origem ).
é possível obter uma expressão para o vetor campo elétrico a partir do resultado do item ? Justifique sua resposta e determine as expressões para as componentes do campo elétrico para as quais a operação proposta seja possível.
Ver solução completaQuestão 108
Considere um disco de raio carregado uniformemente com carga . Calcule o potencial elétrico ao longo do eixo a uma distancia do centro do disco. Adote potencial nulo no infinito.
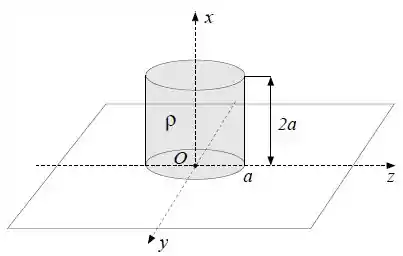
Calcule o potencial elétrico no ponto com coordenadas devido a um cilindro de altura e raio de base , uniformemente carregado com densidade volumétrica de carga . A base do cilindro está contida no plano e seu eixo coincide com o eixo , conforme a figura. Sugestão: Decomponha o cilindro em discos elementares de altura e utilize o resultado do item (a).
Questão 109
Considere um disco de plástico perfurado de raio menor e raio maior , uniformemente carregado com uma densidade de carga :
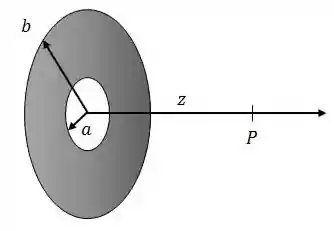
(a) Calcule o potencial elétrico gerado por esta distribuição em um ponto sobre o eixo de simetria perpendicular ao plano que contém o disco e passa por seu centro geométrico. Tome o potencial no infinito como zero!
Ver solução completaQuestão 110
Considere um fio retilíneo de comprimento , com densidadade linear de carga , posicionado conforme mostra a figura.
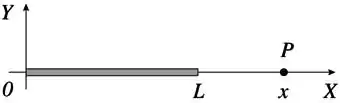
(a) Calcule o potencial elétrico em um ponto sobre a parte positiva do eixo de coordenadas , com . Assuma o potencial nulo no infinito.
(b) Calcule a componente do campo elétrico no ponto .
(b) Qual é o trabalho de uma força externa para trazer uma carga de prova do infinito até o ponto ?
Ver solução completaQuestão 112
Uma esfera condutora está carregada e o potencial elétrico em sua superfície é de (em relação ao infinito). Se o raio da esfera fosse o dobro, mas com a mesma quantidade de carga, qual seria o potencial na sua superfície em relação ao infinito?
Questão 113
Uma barra fina e isolante de comprimento é posicionada sobre o eixo de um sistema de coordenadas com seu centro sobre a origem, como mostrado na figura abaixo.

Ela possui uma densidade linear de carga não-uniforme dada por , onde é uma constante positiva. Considere que o potencial elétrico é nulo no infinito.
Determine o potencial elétrico em um ponto sobre o eixo , a uma distância da origem.
Obtenha uma expressão assintótica para o resultado do item no limite . Interprete o resultado.
No formulário tem essa integral simpática (nem tanto):
E também tem essa aproximação:
Ver solução completaQuestão 114
Uma esfera condutora de raio possui uma carga total . Seja a distância radial medida desde o centro da esfera.
a) Calcule o módulo do vetor campo elétrico nas regiões e .
b) Calcule o potencial elétrico nas regiões e .
Ver solução completaQuestão 115
Uma esfera metálica carregada com uma carga se situa dentro de uma casca esférica condutora com carga . A esfera interna possui raio e a casca externa possui raio , com . O espaço entre as esferas é o vácuo.
a) Calcule o potencial elétrico em todos os pontos.
b) Desenhe o gráfico do potencial, destacando valores em relação a cada um dos corpos.
Ver solução completaQuestão 116
Considere a coroa circular da figura 1, raio interno e raio externo , com densidade superficial de carga não uniforme dada pela função , onde é uma constante positiva e é a distância a partir do centro. Considere também o ponto no eixo da coroa, à altura do centro. A figura 2 mostra um anel de raio e carga total . Sabe-se que o potencial geral em pelo anel é dado por
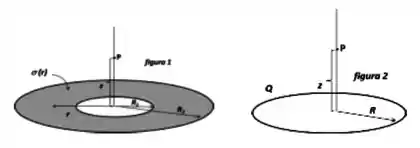
a) Adaptando o resultado do potencial do anel, utilize a relação para encontrar o potencial gerado pela coroa circular em .
Suponha, agora, que uma carga pontual , inicialmente em repouso no ponto , é solta e cruze a origem , submetida à força elétrica (desconsidere, portanto, a força de gravidade).
b) Para que isso aconteça, que sinal deve ter a carga e qual será a sua energia cinética final ao cruzar a origem?
Desconsidere, agora, a carga e suponha que o potencial geral pela coroa circular em tenha o seguinte valor: . Imagine uma casca esférica isolante de espessura infinitesimal seja colocada envolvendo toda a coroa circular e também o ponto . A casca esférica possui uma carga uniformemente distribuída em sua superfície.
c) Calcule que raio a casca esférica deve ter para que o potencial total em seja nulo. (Considere ).
Ver solução completaQuestão 117
Uma esfera maciça condutora, de raio e carga , é concêntrica com uma camada esférica condutora carregada com uma carga que tem raio interno e raio externo .
Determine o campo elétrico para as regiões , , e .
Encontre o potencial elétrico para essas regiões do espaço;
Qual deve ser a razão entre a carga da esfera e a carga da camada condutora para a qual o potencial eletrostático do sistema no centro comum da esfera e da camada seja igual ao potencial do sistema no infinito?
Ver solução completaQuestão 118
Considere o gráfico da figura abaixo.
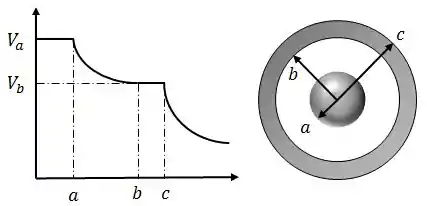
Ele corresponde ao potencial elétrico em função da distância à origem de um sistema de cargas com simetria esférica e raio externo . Para este sistema, responda:
- Qual a intensidade do campo elétrico para ?
- Qual a carga total do sistema?
- Qual o campo elétrico para em função de e das grandezas fornecidas?
Questão 119
Uma esfera não condutora de raio carregada com uma carga , uniformemente distribuída por todo seu volume, é envolvida por uma camada esférica condutora, raios e , carregada com uma carga total , conforme a figura.
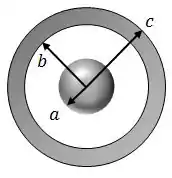
- Use a lei de Gauss para determinar as expressões do vetor campo elétrico em todo espaço: , , e ;
- Calcule a diferença de potencial entre um ponto da superfície da esfera e um ponto da superfície interna da camada, isto é, ;
- Quais são as cargas sobre as superfícies interna e externa da camada condutora?
Questão 120
Um disco de raio oco, de raio interno e raio externo conforme mostrado na figura abaixo, possui uma distribuição superficial de carga expressa por , onde é uma constante com unidade de carga por unidade de área.
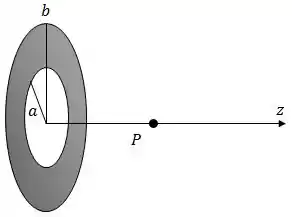
Dado:
Determine:
A carga total no disco, em função de e ;
O potencial elétrico sobre o eixo do disco a uma distância de seu centro;
A energia potencial elétrica necessária para colocar uma carga , num ponto de coordenada ao longo do eixo do disco a uma distância , trazida do infinito;
Ver solução completaQuestão 121
Uma casca esférica condutora de raio interno e externo é concêntrica a uma casca esférica condutora fina de raio . A casca esférica fina tem uma carga total e a carga total da casca externa é zero, sendo que ambas estão isoladas.
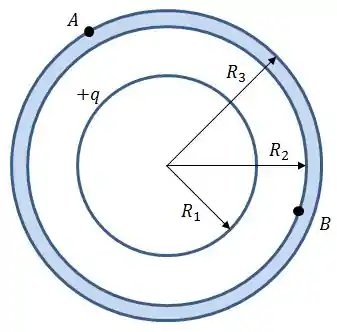
Determine a densidade de carga em cada superfície da camada;
Encontre as expressões para o potencial elétrico em todo espaço: , , e . Suponha que no infinito;
Calcule a diferença de potencial entre os ponto e na camada esférica externa;
Ver solução completaQuestão 122
O anel de raio mostrado na Figura contém uma carga total uniformemente distribuída. O potencial elétrico devido ao anel em um ponto qualquer do eixo é:
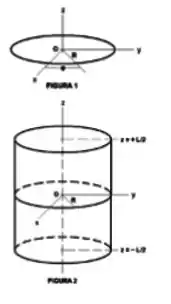
(a) Use o resultado acima para determinar uma expressão para o potencial elétrico em um ponto arbitrário do eixo devido a um disco de raio carregado com a densidade superficial , onde é a distância de um ponto do disco ao seu centro (Figura ).
Suponha agora que a casca cilíndrica da Figura seja longa e que os pontos de interesse sejam externos a ela e próximos da sua superfície, mas afastados de suas extremidades.
(b) Determine o vetor campo elétrico em um ponto de interesse arbitrário, em função da distância ao eixo da casca cilíndrica.
(c) Use o resultado do item anterior para determinar a diferença entre os potenciais elétricos (ddps) de pontos de interesse situados em e .
Ver solução completaQuestão 123
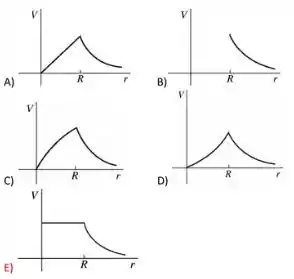
7 - Uma esfera condutora de raio R está carregada positivamente e está afastada de quaisquer outras cargas. Qual dos gráficos abaixo representa melhor o potencial produzido pela esfera em função de r (distância até o centro da esfera)? Considere o potencial no infinito como sendo nulo.
Questão 124
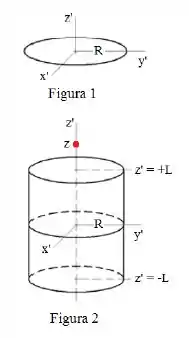
O anel de raio mostrado na Figura 1 contém uma carga total uniformemente distribuída.
a) Determine uma expressão para o potencial elétrico devido ao anel em um ponto qualquer do eixo ;
b) Determine o potencial elétrico devido à casca cilíndrica de e carregada com uma densidade superficial de carga uniforme, mostrada na Figura 2, no ponto do mesmo eixo;
Questão 125
Um fio retilíneo, fino, muito longo, possui densidade linear de carga constante . Ao deslocarmos uma partícula de carga , desde um ponto a uma distância até outro ponto a uma distância de tal fio, qual é o trabalho realizado pela força elétrica do fio sobre a partícula?
.
.
.
.
.
.
Ver solução completaQuestão 126
Oito gotas de água idênticas estao todas ao mesmo potencial , relativo ao potencial nulo no infinito. Elas se juntam para formar uma única gota esférica, cujo potencial deve ser:
a)
b)
c)
d)
e)
Ver solução completaQuestão 127
Assumindo a referência de que potencial elétrico é nulo no infinito, o cálculo do potencial elétrico no centro de um anel de raio uniformemente eletrizado com carga elétrica é zero. Verdadeiro ou falso?
Ver solução completaQuestão 128
Uma esfera maciça e isolante de raio igual a está uniformemente carregada em todo
seu volume com uma carga total de . Qual o valor do potencial elétrico na superfície da esfera se tomarmos como referência para o potencial nulo o seu centro?
- 225V
Questão 129
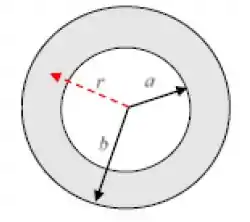
Uma coroa circular isolante, plana, com raio interno e raio externo ,possui uma quantidade total de carga . Esta carga é distribuída de maneira não uniforme sobre a coroa circular, de tal forma que a densidade superficial é dada por: , onde é uma constante positiva e é a distância do centro da coroa circular até qualquer ponto sobre ela, como mostrado na figura. Considere que o potencial é nulo no infinito ( no infinito).
- Calcule a carga total na coroa circular em função de e dos raios e .
- Calcule o potencial no centro da coroa circular, deixando a sua expressão em função de e dos outros dados do problema.
Questão 130
A figura abaixo ilustra um capacitor cilíndrico de comprimento , composto por duas cascas cilíndricas coaxiais. A casca interna tem raio e carga , e a casca externa tem raio e carga . Sabe-se que e que . Existe vácuo no espaço entre as placas (), cuja constante de permissividade elétrica é dada por .
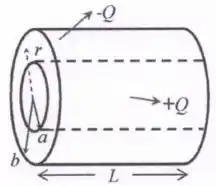
- Calcule o módulo do campo elétrico na região entre as cascas .
- Calcule a diferença de potencial elétrico entre as cascas.
- Calcule a capacitância de tal capacitor cilíndrico.
- Se o espaço entre as placas é completamente preenchido por um material dielétrico de constante dielétrica , determine a nova capacitância deste sistema.
Questão 131
Considere um disco de plástico perfurado de raio menor e raio maior , uniformemente carregado com uma densidade de carga :
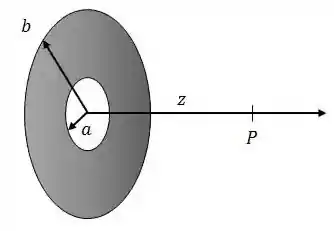
(b) Calcule o campo elétrico em .
Ver solução completaQuestão 132
Qual o potencial eletrostático no centro de um anel metálico de raio e carga ?
- .
- .
- .
- .
- .
Questão 133
Uma esfera condutora de raio , em equilíbrio eletrostático, possui carga . Uma casca esférica espessa, condutora, de raio interno e raio externo , concêntrica à esfera, possui carga , como mostra a figura abaixo. Considerando o potencial elétrico nulo no infinito, a que distância finita do centro da esfera o potencial também é nulo?
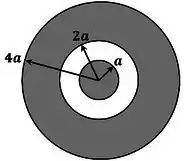
(a)
(b)
(c)
(d)
(e)
(f) Não há nenhuma posição, a uma distância finita do centro da esfera, em que o potencial seja nulo.
Ver solução completaQuestão 134
Considere um disco de raio com uma carga uniformemente distribuída.
a) Calcule o potencial num ponto do eixo do disco, a uma distância do centro.
b) Qual é a diferença de potencial entre o centro do disco e um ponto sobre seu eixo a uma distância do centro?
c) Utilizando a relação entre campo elétrico e o potencial, deduza uma expressão para o campo elétrico do disco no ponto do item (a).
d) Qual é o trabalho necessário para trazer uma carga de prova desde o infinito até o centro do disco?
Dado: potencial de um anel com carga , em um ponto do eixo do anel, a uma distância do centro:
Ver solução completa