Fasores e Circuitos RLC
Produzido por Bruno SoaresTeoria
Introdução
Agora que já sabemos tudo sobre corrente alternada, bora ver como fica o circuito RLC em série quando alimentado por um gerador de corrente alternada!
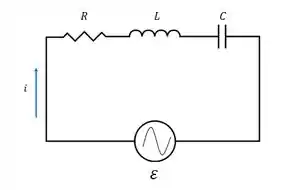
Temos as três componentes alinhadas em série com uma fonte de CA, como será que calcularemos a voltagem e a corrente para cada uma das componentes nesse caso??
A fem aplicada a esse circuito é:
Como os componentes estão em série, a mesma corrente passa por todos eles, ela é dada por:
Para determinar a amplitude da corrente e a constante de fase , é de grande ajuda utilizar os diagramas de fasores. Vamos ver como cada fasor se comporta, começando pela corrente!
Corrente
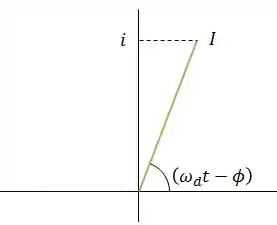
Em um instante qualquer , temos que o fasor que representa a corrente, seu comprimento é a amplitude da corrente, a sua projeção no eixo vertical nos da a corrente para aquele instante e o ângulo de rotação é a fase .
Vamos agora ver como ficam os fasores das tensões nos terminais dos componentes, em relação ao fasor da corrente!
Tensões
Bom agora vamos fazer uma breve análise das tensões em conjunto e após isso esboçar os gráficos delas.
A tensão no resistor é sempre na mesma fase da , e tiramos isso usando a lei de Ohm:
Já a tensão no indutor é dada por:
E como o circuito é em série:
E com
Onde
Por fim temos que trabalhar com a mesma trigonométrica então usaremos a identidade:
Então a voltagem do indutor fica adiantada em relação a do resistor:
Vamos analisar a voltagem do capacitor agora, lembrando que:
Integrando a equação da corrente teremos:
Como , e :
Usando a identidade:
Temos:
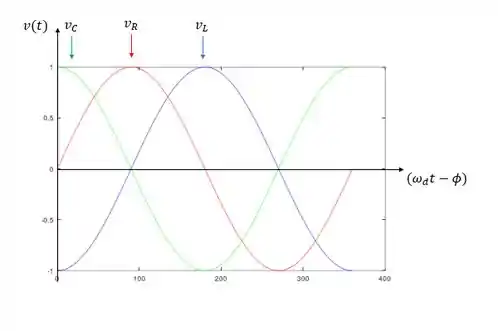
Beleza, enfim definimos as três equações para a mesma trigonométrica. Se por acaso esses caras tivessem a mesma amplitude o gráfico deles em função do tempo ficaria desse jeito, se mostrados juntos:
E o gráfico no domínio da frequência mais conhecido como diagrama fasorial ficaria desse jeito aqui:
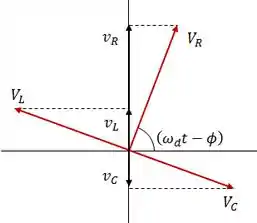
Podemos fazer algumas observações:
- A tensão no resistor e a corrente estão em fase, ou seja, o ângulo de rotação do fasor é o mesmo de .
- A corrente está adiantada em relação à tensão no capacitor, ou seja, o ângulo de rotação do fasor é o mesmo da corrente menos .
- A corrente está atrasada em relação à tensão no indutor, ou seja, o ângulo de rotação no fasor é o mesmo da corrente mais .
Força Eletromotriz
Por último, veremos o fasor que representa a força eletromotriz:
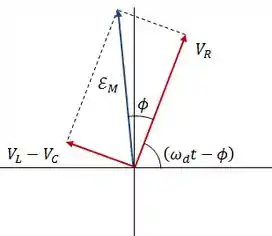
Temos que o comprimento do fasor é o valor absoluto da força eletromotriz, a sua projeção no eixo vertical é a força motriz daquele instante e o angulo de rotação do fasor é !
O fasor é a soma vetorial dos fasores , e . Assim, de acordo com o diagrama de fasores, podemos dizer que:
Sabendo que , e , podemos escrever a amplitude da corrente como:
Onde o denominador define uma nova grandeza, chamada impedância:
E pra facilitar a nossa vida vamos conhecer o triângulo da impedância que ajuda a relacionar as resistências e a reatância com a impedância e a constante de fase .
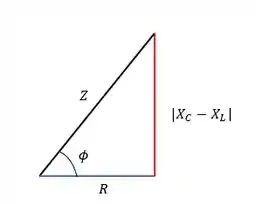
O módulo entra pra que a geometria do triângulo seja sempre positiva. A partir dele podemos através do teorema de Pitágoras calcular a impedância sem ter que decorar de fato a equação e também calcular a constante de fase.
Podemos usar a trigonometria por exemplo, e calcular a constante de fase fazendo a inversa da tangente.
Onde e .
Um outro cara importante, e que veremos melhor nos próximos tópicos é o fator de potência, e ele é dado pelo cosseno do ângulo de fase.
Esse fator define o quanto de potência efetiva é transmitida para uma rede.
Analisando, temos que:
- : Neste caso, o circuito é mais indutivo do que capacitivo. Por termos positivo, temos que o fasor está atrasado em relação ao fasor !
- Neste caso, o circuito é mais capacitivo do que indutivo. Por termos negativo, temos que o fasor está adiantado em relação ao fasor !
- : Neste caso, o circuito está em ressonância, por ser igual a zero, temos que e estão em fase!
No caso da ressonância, temos que a frequência angular de excitação, ou frequência de ressonância, é dada por:
Na prática
Agora que a gente já tá fera vamos calcular a impedância e montar o diagrama fasorial das tensões desse cara com valores:
Se a indutância mede , a capacitância , a resistência do resistor é e a corrente é dada pela equação:
Calcule as reatâncias indutiva e capacitiva e também a diferença de potencial em cada elemento. Esboce o diagrama fasorial, calcule a impedância e o fator de potência do circuito.
Começaremos pelas reatâncias, a partir delas encontraremos tudo o que precisamos:
Olhando pra equação temos:
A reatância capacitiva é dada por:
E a reatância indutiva é:
Como o circuito é mais capacitivo que indutivo.
Partindo pras equações da voltagem, a gente sabe que a voltagem no resistor é tranquila, dada pela lei de Ohm, e como o circuito é em série a corrente é a mesma em todos os pontos.
E daqui tiramos a amplitude da voltagem do resistor:
A voltagem do capacitor a gente já viu que é atrasada em relação a voltagem do resistor, portanto, só precisaremos do seu módulo.
E a equação que é atrasada de fica:
Para o indutor o processo é bem parecido:
Onde:
E a equação da voltagem do indutor fica:
Por fim o diagrama fasorial das tensões vai ficar desse jeitinho aqui:
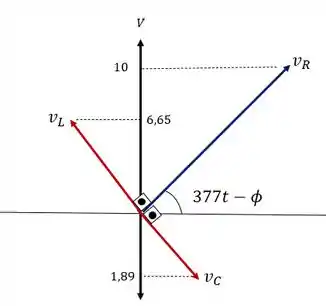
E para calcular a impedância a gente faz o Pitágoras usando o triângulo:
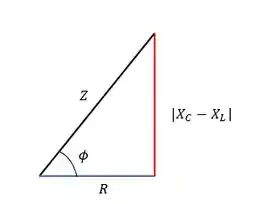
Então é isso calculamos a impedância do circuito, que é como a resistência equivalente pra esse tipo de circuito.
E o fator de potência pelo triângulo fica mole né?
Então a potência efetiva que a rede recebe é 0,44 vezes a potência aparente.
Bora fazer mais exercícios pra ficar fera nisso beleza?
Força Eletromotriz
Na prática
Exercícios Resolvidos
Exercício Resolvido #1
UNICAMP – Física III – Prova 3 – 2008.2 – Noturno – Questão nº4.
No circuito abaixo, a corrente é dada por e a fonte de é . A reatância capacitiva deste circuito é .
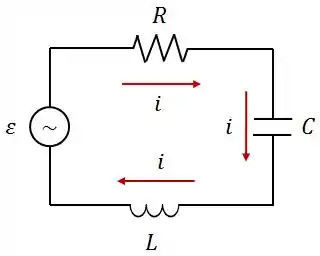
Dados: , , e , calcule:
A impedância do circuito;
O valor da indutância;
A constante de fase ;
A potência média dissipada nos resistor;
A frequência da fonte para a qual a potência média dissipada em será máxima;
Passo 1
A impedância do circuito;
A impedância do circuito pode ser calculada simplesmente por:
Passo 2
O valor da indutância;
Opa! Vamos lá!
A impedância do circuito pode ser calculada também por:
Onde:
Sendo que o problema já nos deu , , e nós acabamos de calcular ... já viu que isso vai dar samba?
Isolando o daquela equação, teremos:
Agora é só substituir os valores:
Passo 3
A constante de fase ;
O ângulo de fase é dado por:
Onde .
Passo 4
A potência média dissipada nos resistor;
A potência dissipada no resistor é dada por:
Mas como a corrente varia com o tempo, a potência média dissipada é dada por:
Onde é o valor quadrático médio da corrente, dado por:
Logo:
Passo 5
A frequência da fonte para a qual a potência média dissipada em será máxima;
A potência média dissipada em será máxima quando a frequência for igual à frequência de ressonância.
Onde .
Resposta
Exercício Resolvido #2
UFF – Lista – Questão nº7.
Este circuito de corrente alternada em série, com frequência angular , descrito pelo gráfico de fasores abaixo.
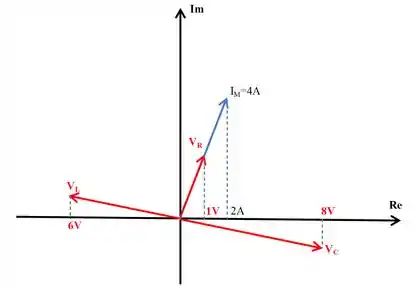
Determine a frequência de ressonância do circuito.
Qual é a diferença de fase entre a corrente e a voltagem na fonte?
Determine a impedância do circuito.
Esboce o gráfico de fasores de todas as voltagens e da corrente para quando o sistema entra em ressonância.
Passo 1
Para resolver essa questão, vamos começar determinando os valores de , , . Como , o ângulo entre o vetor e o eixo horizontal é . Portanto, esse é o mesmo ângulo entre e o eixo horizontal:
Analogamente, o ângulo entre e o eixo horizontal é :
E o ângulo entre e o eixo horizontal é :
Agora que temos os valores das tensões e da amplitude da corrente, podemos determinar as impedâncias e , sabendo o valor de , podemos determinar o valor da indutância e da capacitância.
Para a indutância, temos:
Analogamente para a capacitância:
Agora que sabemos e , podemos determinar a frequência angular de ressonância:
Passo 2
Para determinar a constante de fase entre a tensão e a corrente, vamos primeiro terminar as componentes da tensão:
Logo, a resultante da tensão é:
Para determinar o ângulo entre e , podemos usar a seguinte relação:
Passo 3
Para determinar a impedância, podemos usar a seguinte relação:
substituindo os valores, temos:
Passo 4
Quando o circuito entra em ressonância, temos que , logo, a tensão , que é a soma vetorial das tensões dos dispositivos no circuito, é igual à , e portanto, está em fase com a corrente. O diagrama fasorial, quando o circuito entra em ressonância é:
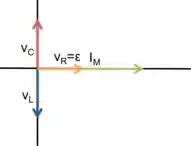
Resposta
Exercício Resolvido #3
PUCRIO – Física III – Prova 3 – 2014.2 – Questão nº3.
No circuito de corrente alternada abaixo sabe-se que o valor quadrático médio da diferença de potencial . Além disso, sabe-se que a amplitude da d.d.p entre os pontos e é dada por: .
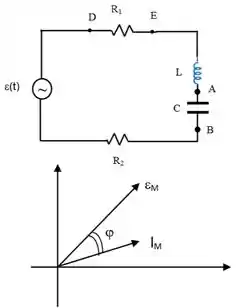
São conhecidos também os valores dos seguintes componentes:
Considerando o diagrama de fasores do circuito e sabendo que escreva a expressão de .
Determine o valor da capacitância .
Determine o valor do resistor .
Pelo gráfico dos fasores o circuito não está em ressonância. Para que isso aconteça é preciso aumentar ou diminuir o valor de ? Justifique as suas afirmações.
Uma vez estabelecida a ressonância no circuito, qual serão os novos valores das amplitudes de e ?
Passo 1
Precisamos determinar a diferença de potencial nos terminais do capacitor, para isso, precisamos lembrar, que em um circuito RLC, temos que no diagrama de fasores, a corrente está adiantada em relação à tensão no capacitor. Então, a tensão no capacitor varia da seguinte forma:
Substituindo os valores, temos:
Passo 2
Precisamos determinar o valor da capacitância, para isso, iremos usar as seguintes relações:
Substituindo na segunda equação, temos:
Nós sabemos o valor máximo de , precisamos determinar , para isso, vamos usar a informação dada no enunciado, temos que , ou seja:
A corrente máxima será:
Agora é só substituir todos os valores na seguinte equação e correr pro abraço!
Passo 3
Para determinar a resistência , precisamos lembrar que está sempre em fase com a corrente , portanto, a componente da tensão total é a indicada na fórmula abaixo:
Além disso, sabemos que, como os resistores estão em série, temos:
Substituindo na primeira equação, temos:
Substituindo os valores, temos:
Passo 4
Para um circuito RLC, temos que a ressonância ocorre quando:
Vamos determinar ambas as reatâncias para avaliar a situação:
Reatância capacitiva:
Reatância Indutiva:
Temos então que , portanto o circuito apresenta comportamento capacitivo, para que as reatâncias se igualem, é preciso que o valor de aumente, podemos ver isso olhando para as definições das reatâncias, é diretamente proporcional à , enquanto é inversamente proporcional à .
Passo 5
Para determinar os novos valores de e para a nova situação, precisamos primeiro determinar o novo valor máximo de corrente:
Para :
Para :
Onde é:
Substituindo:
Resposta
O valor de deve aumentar.
Exercício Resolvido #4
PUCRIO – Física III – Prova 3 – 2015.1 – Questão nº3.
O circuito em série mostrado na Figura 1 é alimentado pela fonte de corrente alternada onde , , , , e .
Determine os valores de e , assim como dos valores máximos das tensões no resistor, indutor e capacitor.
Com base nestes valores, represente o diagrama fasorial para o circuito, indicado se ele é indutivo ou capacitivo.
Em seguida, suponha que a mesma fonte , onde e , é conectada a um outro circuito série com , , fixos mas desconhecidos. Quando , medem-se e . Quando , medem-se e .
Com base nos dados fornecidos imediatamente acima determine os valores de , e .
Passo 1
Determine os valores de e , assim como dos valores máximos das tensões no resistor, indutor e capacitor.
As tensões máximas no resistor, indutor e no capacitor são dadas por:
Onde:
Então precisamos começar calculando , , e .
Os dados do problema são:
Logo:
Agora podemos calcular e as voltagens máximas.
Passo 2
O problema também pede para calcularmos a diferença de fase , que é dada por:
Passo 3
Com base nestes valores, represente o diagrama fasorial para o circuito, indicado se ele é indutivo ou capacitivo.
Como estamos trabalhando com um circuito , precisamos lembrar de algumas coisas:
- A tensão no resistor e a corrente estão em fase, ou seja, o ângulo de rotação do fasor é o mesmo de .
- A corrente está adiantada em relação à tensão no capacitor, ou seja, o ângulo de rotação do fasor é o mesmo da corrente menos .
- A corrente está atrasada em relação à tensão no indutor, ou seja, o ângulo de rotação no fasor é o mesmo da corrente mais .
Assim, o diagrama fasorial terá essa cara:
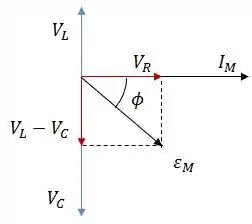
Como , o diagrama é capacitivo.
Passo 4
Com base nos dados fornecidos imediatamente acima determine os valores de , e .
O problema diz que, quando , e .
Se a diferença de fase é nula, corresponde à frequência de ressonância, logo, para :
Além disso, na ressonância, , logo:
Passo 5
Para , medem-se e .
Daqui podemos tirar que:
Do passo anterior, descobrimos que e . E, de acordo com o enunciado, , logo:
Agora podemos descobrir, também, , usando a frequência de ressonância:
Portanto:
Resposta
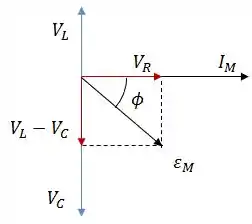
O diagrama é capacitivo.
Exercício Resolvido #5
UNICAMP – Física III – Prova 3 – 2008.2 – Noturno – Questão nº4.
No circuito abaixo, a corrente é dada por e a fonte de é . A reatância capacitiva deste circuito é .
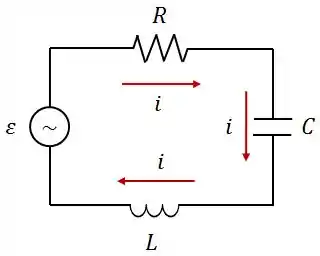
Dados: , , e , calcule:
A impedância do circuito;
O valor da indutância;
A constante de fase ;
A potência média dissipada nos resistor;
A frequência da fonte para a qual a potência média dissipada em será máxima;
Passo 1
A impedância do circuito;
A impedância do circuito pode ser calculada simplesmente por:
Passo 2
O valor da indutância;
Opa! Vamos lá!
A impedância do circuito pode ser calculada também por:
Onde:
Sendo que o problema já nos deu , , e nós acabamos de calcular ... já viu que isso vai dar samba?
Isolando o daquela equação, teremos:
Agora é só substituir os valores:
Passo 3
A constante de fase ;
O ângulo de fase é dado por:
Onde .
Passo 4
A potência média dissipada nos resistor;
A potência dissipada no resistor é dada por:
Mas como a corrente varia com o tempo, a potência média dissipada é dada por:
Onde é o valor quadrático médio da corrente, dado por:
Logo:
Passo 5
A frequência da fonte para a qual a potência média dissipada em será máxima;
A potência média dissipada em será máxima quando a frequência for igual à frequência de ressonância.
Onde .
Resposta
Exercício Resolvido #6
UNICAMP – Física III – Prova 3 – 2012.1 – Manhã – Questão nº4.
Um circuito de corrente alternada é constituído de uma indutância de em série com uma resistência de alimentados por um gerador alternado de com frequência de .
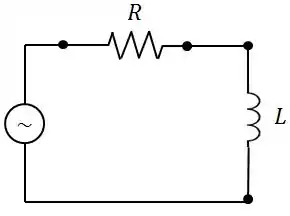
- Qual o fator de potência do circuito?
- Qual deve ser a capacitância de um capacitor que, colocado em série no circuito, tornaria este fator de potência unitário?
- Qual seria, agora, o valor da corrente com a introdução deste capacitor?
- Quais seriam as expressões das tensões em função do tempo no capacitor e no indutor?
Passo 1
- Qual o fator de potência do circuito?
- Qual deve ser a capacitância de um capacitor que, colocado em série no circuito, tornaria este fator de potência unitário?
- Qual seria, agora, o valor da corrente com a introdução deste capacitor?
- Quais seriam as expressões das tensões em função do tempo no capacitor e no indutor?
O fator de potência é dado por:
Onde é o ângulo de fase, dado por:
Mas como se trata de um circuito :
Beleza, então vamos começar calculando que é a reatância indutiva, dada por:
Onde e . Logo:
Passo 2
Agora podemos calcular o ângulo de fase pra encontrar o fator de potência:
O fator de potência será:
Passo 3
Vamos analisar aqui... como o fator de potência é dado por:
Ele será unitário quando , logo, quando e .
Portanto:
Onde e . Logo:
Passo 4
O problema nos diz que:
E podemos associar com por:
Onde é a impedância, dada por:
Sendo .
Agora sim.
Passo 5
Bom, aqui vale a pena dividir o problema em dois e calcular em cada um separadamente, começando pela indutor, já que já calculamos .
- Indutor:
- Capacitor:
A tensão no indutor é dada por:
Então vamos começar escrevendo a expressão de .
Como já vimos, , e podemos usar para encontrar :
Logo:
Em módulo:
Passo 6
Já vimos que, para o capacitor escolhido:
Podemos dizer então que:
Resposta
a.
b.
c.
d.
Exercício Resolvido #7
PUCRIO – Física III – Prova 3 – 2013.1– Questão nº3.
Um potenciômetro (dimmer) é um dispositivo que permite variar a intensidade luminosa de uma lâmpada. Estes dispositivos são compostos por uma bobina de indutância variável em série com uma lâmpada(Figura ).
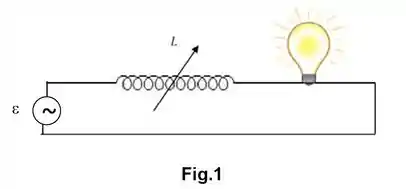
O circuito é alimentado por um gerador alternado com uma eficaz e uma frequência angular . Considere que a lâmpada utilizada é de de potência e que a sua resistência elétrica seja independente da temperatura.
Calcule qual deve ser o valor mínimo da indutância para que a potencia média dissipada na lâmpada seja máxima .
Calcule qual deve ser o valor máximo da indutância para que a potencia média dissipada pela lâmpada seja .
Se no lugar do gerador de alternada fosse inserida uma bateria em corrente continua , qual deveria ser o valor da tensão para que, decorrido um tempo muito longo, a potência dissipada na lâmpada fosse de ?
Considere novamente o circuito da Figura . Agora a lâmpada é substituída por um resistor do mesmo valor e no circuito é inserido em série um capacitor .
Considerando que a indutância possui o valor máximo calculado no item desenhe o diagrama de fasores do circuito. A corrente que passa no circuito está adiantada ou atrasada em relação à tensão do gerador?
Mudando o valor da indutância entre os limites calculados nos itens e é possível fazer com que o circuito entre em ressonância? Em caso de resposta negativa justifique. Em caso de resposta afirmativa calcule o valor de para que isso aconteça.
Passo 1
Para um circuito RLC, temos que a potência dissipada é dada pela seguinte fórmula:
Onde e , lembrando que . Substituindo:
Para que , como o valor de e não variam, a única maneira de ter a potência máxima é quando for mínimo, ou seja, , nesse caso, , logo, o valor da resistência será:
Passo 2
Para , usando a relação anterior, temos:
Substituindo e os outros valores, temos:
Passo 3
Para um tempo muito longo, temos que o indutor irá se comportar como um fio normal, sem resistência, logo, a potencia dissipada será:
Passo 4
Agora, temos um novo circuito, onde , além disso, temos um novo componente, o capacitor, para esse circuito, vamos determinar as reatâncias:
Logo, o diagrama pode ser representado da seguinte forma:
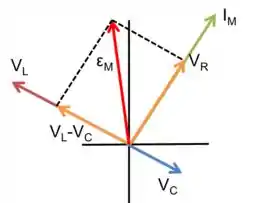
Logo, a corrente está atrasada em relação à tensão!
Passo 5
Para que o circuot0 entre em ressonância, precisamos que:
Substituindo os valores, temos:
Portanto , existe sim um valor de , entre e para que o circuito entre em ressonância!
Resposta
Ver figura. Corrente atrasada em relação à tensão.
Exercício Resolvido #8
Unicamp – Física III – Prova 3 – 2017.2 – Questão 9
Considere o circuito abaixo. Um resistor , um capacitor e um indutor são ligados em paralelo a uma fonte de tensão alternada. Qual(is) das seguintes afirmações é(são) correta(s)?
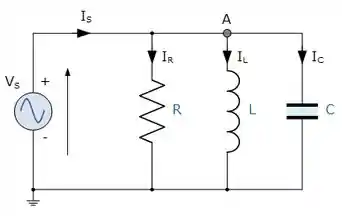
I. A soma das correntes instantâneas em cada elemento deve ser igual à corrente instantânea fornecida pela fonte.
II. A soma das voltagens instantâneas através de cada elemento deve ser igual à voltagem da fonte;
III. A voltagem instantânea através de está defasada de em relação à voltagem através de .
IV. A voltagem instantânea através de está defasada de em relação à voltagem através de .
V. Toda a energia é dissipada pelo resistor.
(a) somente II, IV e V são corretas.
(b) somente II e V são corretas.
(c) somente I, III e V são corretas.
(d) somente I, IV e V são corretas.
(e) somente I e V são corretas.
Passo 1
Vamos analisar cada uma das afirmações:
I. Verdadeiro, pois os componentes estão em paralelo.
II. Falso, pois os componentes estão em paralelo! Nesse caso, as voltagens instantâneas são iguais.
III. Falso, as voltagens nos componentes são iguais.
IV. Falso, as voltagens nos componentes são iguais.
V. Verdadeiro.
Resposta
(e) somente I e V são corretas.
Exercício Resolvido #9
Unicamp – Física III – Prova 3 – 2017.2 – Questão 8
Um gerador AC produz (rms) a uma frequência de . Ele é ligado em série a um resistor com e um indutor com . A corrente rms é:
(a) e adiantada de em relação à fem.
(b) e atrasada de em relação à fem.
(c) e atrasada de em relação à fem.
(d) e atrasada de em relação à fem.
(e) e adiantada de em relação à fem.
Passo 1
A reatância no indutor é dada por:
A impedância do circuito será:
Passo 2
Logo, a corrente máxima é dada por:
.
A corrente rms será:
Passo 3
A constante de fase pode ser calculada como:
Logo, a corrente está atrasada de em relação à fem.
Resposta
(c) e atrasada de em relação à fem.