Exercícios de Fasores e Circuitos RLC - Lista de Exercícios Resolvida
Questão 1
Considere o circuito abaixo. Um resistor , um capacitor e um indutor são ligados em paralelo a uma fonte de tensão alternada. Qual(is) das seguintes afirmações é(são) correta(s)?
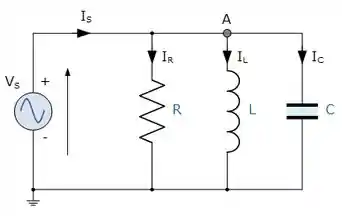
I. A soma das correntes instantâneas em cada elemento deve ser igual à corrente instantânea fornecida pela fonte.
II. A soma das voltagens instantâneas através de cada elemento deve ser igual à voltagem da fonte;
III. A voltagem instantânea através de está defasada de em relação à voltagem através de .
IV. A voltagem instantânea através de está defasada de em relação à voltagem através de .
V. Toda a energia é dissipada pelo resistor.
(a) somente II, IV e V são corretas.
(b) somente II e V são corretas.
(c) somente I, III e V são corretas.
(d) somente I, IV e V são corretas.
(e) somente I e V são corretas.
Ver solução completaQuestão 2
No circuito abaixo, a corrente é dada por e a fonte de é . A reatância capacitiva deste circuito é .
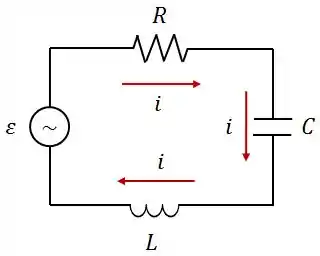
Dados: , , e , calcule:
A impedância do circuito;
O valor da indutância;
A constante de fase ;
A potência média dissipada nos resistor;
A frequência da fonte para a qual a potência média dissipada em será máxima;
Ver solução completaQuestão 3
Um gerador AC produz (rms) a uma frequência de . Ele é ligado em série a um resistor com e um indutor com . A corrente rms é:
(a) e adiantada de em relação à fem.
(b) e atrasada de em relação à fem.
(c) e atrasada de em relação à fem.
(d) e atrasada de em relação à fem.
(e) e adiantada de em relação à fem.
Ver solução completaQuestão 4
Um circuito de corrente alternada é constituído de uma indutância de em série com uma resistência de alimentados por um gerador alternado de com frequência de .
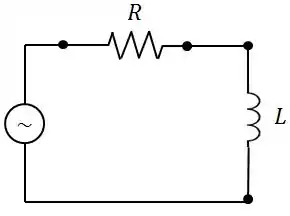
- Qual o fator de potência do circuito?
- Qual deve ser a capacitância de um capacitor que, colocado em série no circuito, tornaria este fator de potência unitário?
- Qual seria, agora, o valor da corrente com a introdução deste capacitor?
- Quais seriam as expressões das tensões em função do tempo no capacitor e no indutor?
Questão 5
No circuito abaixo, a corrente é dada por e a fonte de é . A reatância capacitiva deste circuito é .
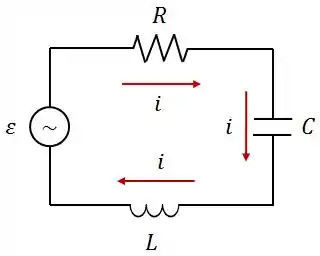
Dados: , , e , calcule:
A impedância do circuito;
O valor da indutância;
A constante de fase ;
A potência média dissipada nos resistor;
A frequência da fonte para a qual a potência média dissipada em será máxima;
Ver solução completaQuestão 6
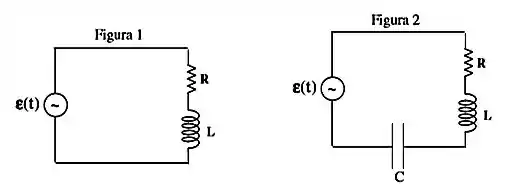
O circuito em série mostrado na Figura 1 é alimentado pela fonte de corrente alternada onde , , , , e .
Determine os valores de e , assim como dos valores máximos das tensões no resistor, indutor e capacitor.
Com base nestes valores, represente o diagrama fasorial para o circuito, indicado se ele é indutivo ou capacitivo.
Em seguida, suponha que a mesma fonte , onde e , é conectada a um outro circuito série com , , fixos mas desconhecidos. Quando , medem-se e . Quando , medem-se e .
Com base nos dados fornecidos imediatamente acima determine os valores de , e .
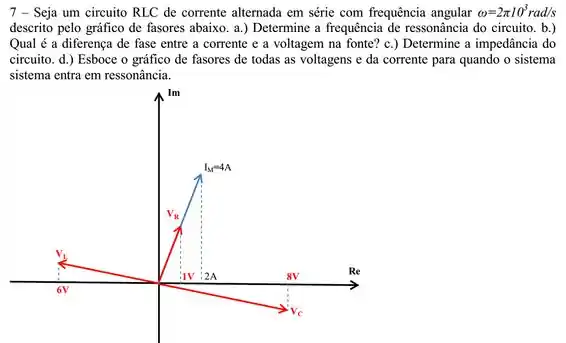
Ver solução completaQuestão 7
Este circuito de corrente alternada em série, com frequência angular , descrito pelo gráfico de fasores abaixo.
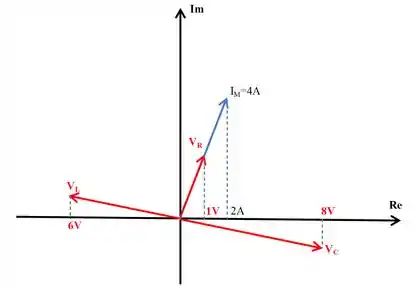
Determine a frequência de ressonância do circuito.
Qual é a diferença de fase entre a corrente e a voltagem na fonte?
Determine a impedância do circuito.
Esboce o gráfico de fasores de todas as voltagens e da corrente para quando o sistema entra em ressonância.
Ver solução completaQuestão 8
No circuito de corrente alternada abaixo sabe-se que o valor quadrático médio da diferença de potencial . Além disso, sabe-se que a amplitude da d.d.p entre os pontos e é dada por: .
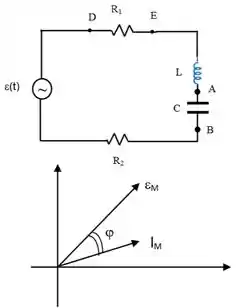
São conhecidos também os valores dos seguintes componentes:
Considerando o diagrama de fasores do circuito e sabendo que escreva a expressão de .
Determine o valor da capacitância .
Determine o valor do resistor .
Pelo gráfico dos fasores o circuito não está em ressonância. Para que isso aconteça é preciso aumentar ou diminuir o valor de ? Justifique as suas afirmações.
Uma vez estabelecida a ressonância no circuito, qual serão os novos valores das amplitudes de e ?
Ver solução completaQuestão 9
Um potenciômetro (dimmer) é um dispositivo que permite variar a intensidade luminosa de uma lâmpada. Estes dispositivos são compostos por uma bobina de indutância variável em série com uma lâmpada(Figura ).
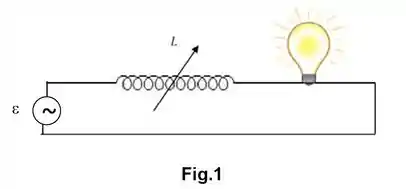
O circuito é alimentado por um gerador alternado com uma eficaz e uma frequência angular . Considere que a lâmpada utilizada é de de potência e que a sua resistência elétrica seja independente da temperatura.
Calcule qual deve ser o valor mínimo da indutância para que a potencia média dissipada na lâmpada seja máxima .
Calcule qual deve ser o valor máximo da indutância para que a potencia média dissipada pela lâmpada seja .
Se no lugar do gerador de alternada fosse inserida uma bateria em corrente continua , qual deveria ser o valor da tensão para que, decorrido um tempo muito longo, a potência dissipada na lâmpada fosse de ?
Considere novamente o circuito da Figura . Agora a lâmpada é substituída por um resistor do mesmo valor e no circuito é inserido em série um capacitor .
Considerando que a indutância possui o valor máximo calculado no item desenhe o diagrama de fasores do circuito. A corrente que passa no circuito está adiantada ou atrasada em relação à tensão do gerador?
Mudando o valor da indutância entre os limites calculados nos itens e é possível fazer com que o circuito entre em ressonância? Em caso de resposta negativa justifique. Em caso de resposta afirmativa calcule o valor de para que isso aconteça.
Ver solução completaQuestão 10
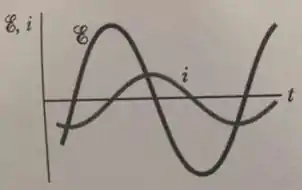
A figura mostra a corrente e a força eletromotriz de um circuito RLC em série. Para aumentar a potência transferida para o resistor, é preciso:
- Aumentar o valor de ;
- Aumentar o valor de ;
- Diminuir o valor de ;
- Aumentar o valor de ;
- Aumentar o valor da frequência da fonte;
Questão 11
Quando um dado indutor é conectado a uma fonte de , que varia senoidalmente com uma amplitude constante e uma frequência de , o valor da corrente é . Qual o valor da corrente se a frequência da fonte for dobrada?
Questão 12
Considere que no circuito abaixo temos , e . Sabendo que a fonte opera com frequência angular de e com uma tensão eficaz (valor quadrático médio) de , determine:
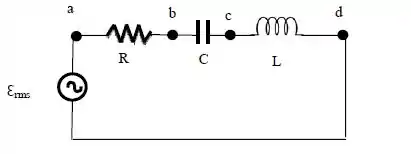
O valor eficaz (quadrático médio) da corrente no circuito.
As tensões eficazes , , , e . (Faça o diagrama de fasores para ajudar no raciocínio).
A potência média fornecida pela fonte e a potência média dissipada em cada elemento do circuito.
O ângulo de fase entre a tensão da fonte e a corrente se a frequência angular mudar para . Neste caso quem está adiantado, a corrente ou a tensão da fonte?
Ver solução completaQuestão 13
Um potenciômetro (dimmer) é um dispositivo que permite variar a intensidade luminosa de uma lâmpada. Estes dispositivos são compostos por uma bobina de indutância variável em série com uma lâmpada(Figura ).
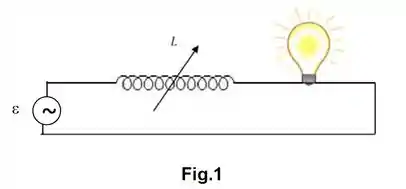
O circuito é alimentado por um gerador alternado com uma eficaz e uma frequência angular . Considere que a lâmpada utilizada é de de potência e que a sua resistência elétrica seja independente da temperatura.
Calcule qual deve ser o valor mínimo da indutância para que a potencia média dissipada na lâmpada seja máxima .
Calcule qual deve ser o valor máximo da indutância para que a potencia média dissipada pela lâmpada seja .
Se no lugar do gerador de alternada fosse inserida uma bateria em corrente continua , qual deveria ser o valor da tensão para que, decorrido um tempo muito longo, a potência dissipada na lâmpada fosse de ?
Considere novamente o circuito da Figura . Agora a lâmpada é substituída por um resistor do mesmo valor e no circuito é inserido em série um capacitor .
Considerando que a indutância possui o valor máximo calculado no item desenhe o diagrama de fasores do circuito. A corrente que passa no circuito está adiantada ou atrasada em relação à tensão do gerador?
Mudando o valor da indutância entre os limites calculados nos itens e é possível fazer com que o circuito entre em ressonância? Em caso de resposta negativa justifique. Em caso de resposta afirmativa calcule o valor de para que isso aconteça.
Ver solução completaQuestão 14
Seja o circuito RLC em série mostrado na figura.
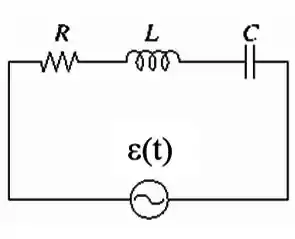
Considerando uma situação geral, com e qualquer, marque verdadeiro ou falso nas seguintes afirmações abaixo:
( ) A energia armazenada no circuito oscila entre e .
( ) A fonte não fornece potência ao circuito: a potência dissipada em é compensada pela variação da energia armazenada em e .
( ) A potência só é dissipada em .
( ) A corrente que passa no indutor está adiantada de e relação à d.d.p no mesmo indutor ().
( ) A tensão no capacitor está adiantada de em relação à tensão no resistor .
No caso das afirmações falsas explique, justificando, o porquê da sua afirmação.
Num dado instante de tempo, o diagrama de fasores do circuito é o seguinte:
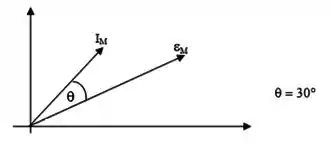
Utilizando apenas as informações do diagrama, calcule a tensão no resistor, .
Para que o circuito entre em ressonância, devemos aumentar ou diminuir a frequência do gerador?
Existe outro método (sem modificar ) que permita atingir a ressonância do circuito? Qual?
Ver solução completaQuestão 15
Um circuito desconhecido, composto somente de elementos escolhidos entre , e , é alimentado por um gerador de corrente alternada cuja fem e dada por , onde e . Realizando uma medida de corrente, se encontra:
Onde .
Após , em que instante de tempo a fem do gerador atinge seu valor máximo pela primeira vez? Em que instante de tempo a corrente atinge o seu valor máximo pela primeira vez? Qual é a diferença de fase entre a tensão do gerador e a corrente?
Desenhe o gráfico dos fasores relativo a este circuito.
Calcule o fator de potencia do circuito. Determine a potencia média fornecida ao circuito.
Com os dados à sua disposição, você poderia dizer se no circuito está presente um resistor? Em caso de resposta afirmativa, calcule o seu valor. Em caso de resposta negativa, justifique a sua afirmação.
O circuito tem um comportamento indutivo ou capacitivo? Justifique o seu raciocínio.
Em função da resposta dada no item anterior, calcule o valor de ou
Ver solução completaQuestão 16
O fluxo magnético através de uma espira circular de diâmetro e resistência , obedece à seguinte equação:
Sabendo que:
- Em , ;
- Em , e ;
- Em , ;
- Em , ;
- Em , ;
- em ;
- em ;
Encontre os valores de e com as unidades corretas e escreva a expressão final para o fluxo magnético (considere e ).
Suponha agora uma nova situação em que o campo magnético através da mesma espira obedeça à seguinte equação: , onde e são constantes a determinar.
Sabendo que nesta nova situação em , e em , encontre os valores das constantes e com as respectivas unidades e escreva a expressão final para o campo magnético e para induzida.
Passo 1
Encontre os valores de e com as unidades corretas e escreva a expressão final para o fluxo magnético (considere e ).
Vamos utilizar as 3 condições que o problema nos deu para encontrar os valores de e , ok?
Por definição, como a área da espira é constante, podemos dizer que , logo:
Derivando o campo magnético em função do tempo, teremos:
Onde:
Portanto:
Passo 2
Beleza, nós já conseguimos determinar quem é , agora vamos ter que resolver o sistema abaixo pra determinar quem é e .
Multiplicando a primeira linha por 3, teremos:
Fazendo a primeira equação menos a segunda, teremos:
Agora, multiplicando a primeira linha por 2 e, depois, fazendo a segunda equação menos a primeira, encontraremos:
Até aqui, beleza, mas quais são as unidades de e ?
Passo 3
Vamos voltar à equação original que o problema nos deu.
Se os três termos estão se somando, eles necessariamente tem as mesmas unidades de medida que, nesse caso, são de fluxo magnético , então basta fazermos uma análise dimensional.
Para , teremos:
Para , teremos:
Finalmente:
Pra finalizar:
Agora sim, acabamos a letra !
Passo 4
Sabendo que nesta nova situação em , e em , encontre os valores das constantes e com as respectivas unidades e escreva a expressão final para o campo magnético e para induzida.
Pra começar, vamos logo determinar as unidades de medida desses caras?
Como a função exponencial é adimensional, deve ter a mesma unidade de , logo:
E como o expoente também deve ser algo adimensional:
Bom, beleza... já podemos nos preocupar só em calcular os valores de e .
A estratégia aqui é a mesma que usamos na letra , vamos usar as condições que o problema nos deu para determinar os valores desses caras:
Finalmente:
Ver solução completaQuestão 17
Um indutor real é formado por uma indutância e uma resistência em série, como mostrado na figura:
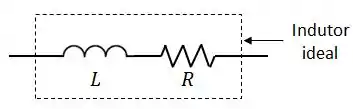
Antes de montar um circuito, queremos descobrir os valores de e . Para isso, conectamos inicialmente o indutor real a uma fonte de tensão contínua de . Após ter esperado um tempo suficientemente longo, medimos, utilizando um multímetro, uma corrente .
Em seguida, conectamos o mesmo indutor real a um gerador de tensão alternada de valor quadrático médio, e com frequência angular . Neste caso, medimos uma corrente quadrática média, .
De posse destas informações determine os valores de e (com os valores numéricos e as unidades).
Em seguida, um capacitor é conectado em série ao indutor real, formando assim um circuito . Este circuito é conectado ao mesmo gerador de tensão alternada do item anterior.
Utilizando os dados à sua disposição, desenhe, nesta condição, o diagrama de fasores do circuito. O circuito tem comportamento capacitivo ou indutivo?
Ver solução completaQuestão 18
Um circuito de corrente alternada é constituído de uma indutância de em série com uma resistência de alimentados por um gerador alternado de com frequência de .
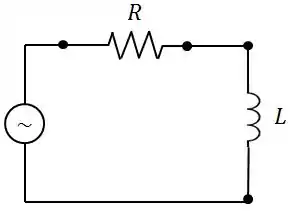
- Qual o fator de potência do circuito?
- Qual deve ser a capacitância de um capacitor que, colocado em série no circuito, tornaria este fator de potência unitário?
- Qual seria, agora, o valor da corrente com a introdução deste capacitor?
- Quais seriam as expressões das tensões em função do tempo no capacitor e no indutor?
Questão 19
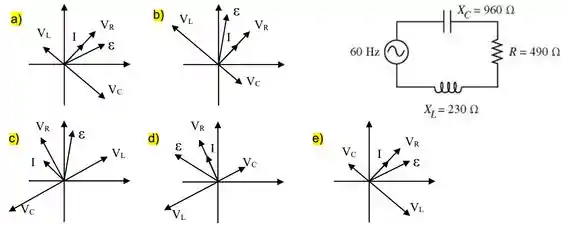
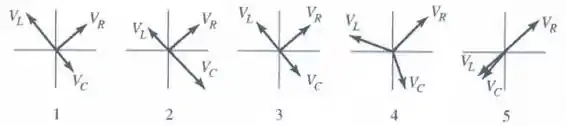
Assinale a figura que descreve corretamente um circuito RLC em termos de fasores.
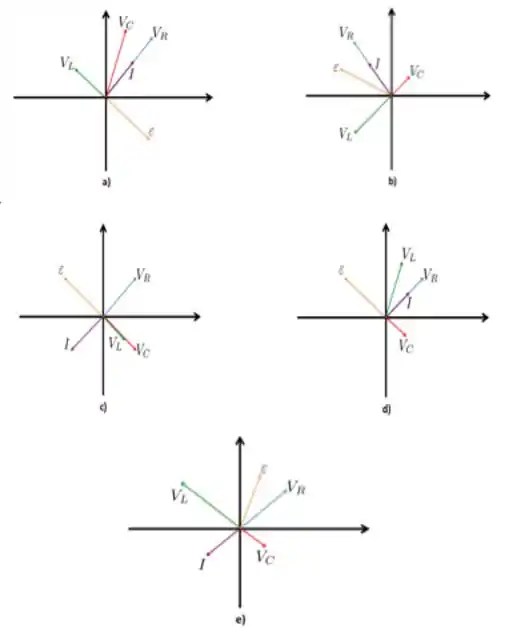
Questão 20
A figura abaixo mostra um circuito de corrente alternada puramente indutivo. A amplitude da fonte é de e sua frequência é de . A corrente máxima no circuito é de . Qual é o valor aproximado da indutância ?
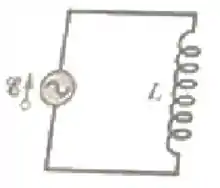
(a) .
(b) .
(c) .
(d) .
(e) .
Ver solução completaQuestão 21
Um circuito RLC em série ligado a um gerador de corrente alternada tem , , e . Na ressonância, a amplitude de voltagem sobre o indutor vale:
- 1000 V
Questão 22
Num circuito RLC com uma fonte alternada, variamos a frequência da fonte e medimos a amplitude da corrente do circuito. Três resistências são trocadas através da chave S, como mostra o circuito. O gráfico mostra a amplitude da corrente versus a frequência dos três resistores , e indicados nas curvas da figura. A relação entre os resistores é:
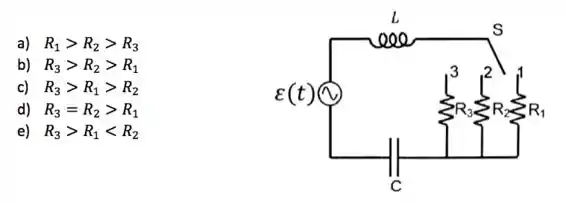
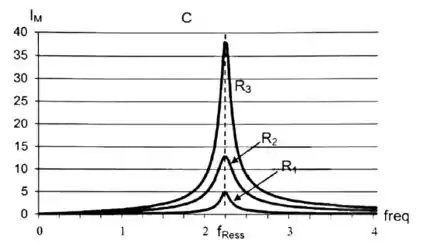
Questão 23
A figura mostra o comportamento da corrente em um circuito RLC em série onde a potência média entregue pela fonte é e a f.e.m. máxima é de . O fator de potência do circuito vale:
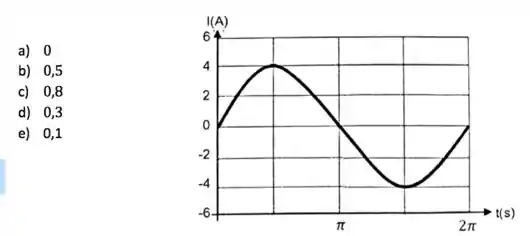
Questão 24
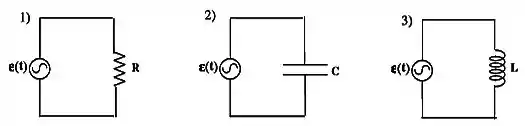
Uma fonte de corrente alternada, que tem a sua variando no tempo da forma , é ligada a três elementos de circuito, como mostram as figuras abaixo.
Para cada um dos circuitos:
- Escreva a equação que relaciona a da fonte com a corrente do circuito.
- Descreva a diferença de fase entre a da fonte e a corrente do circuito.
- Ache corrente em função do tempo.
Questão 25
O circuito da figura é usado para determinar a capacitância do capacitor.
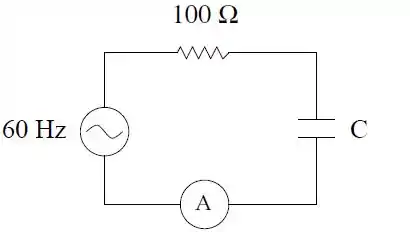
O resistor tem resistência de e a fonte de tensão é um gerador de com frequência de e tensão eficaz de . A leitura do amperímetro que mede o valor eficaz da corrente é .
Faça um diagrama indicando claramente os fasores da corrente e das tensões no gerador, resistor e capacitor. Determine a capacitância do capacitor.
Calcule a potência média consumida pelo circuito e o fator de potência.
Admitindo-se que para tem-se um pico de tensão no gerador, determine a tensão instantânea no capacitor.
Ver solução completaQuestão 26
Aplica-se uma ddp nos terminais de um circuito constituído em série por um indutor de indutância , um capacitor com capacitância e uma resistência .
- Determine a amplitude da voltagem nos terminais do capacitor em termos de e ;
- Determine o valor da capacitância para a qual a amplitude da voltagem nos terminais do capacitor é máxima;
- Determine o valor da capacitância para a qual a amplitude da corrente no circuito é máxima;
Questão 27
Um gerador de de frequência angular alimenta um dispositivo em sérei com um capacitor de . No dispositivo a voltagem está adiantada de radianos em relação à corrente no circuito. A tensão no gerador cujo valor eficaz é de está em fase com a corrente. A corrente no circuito é de .
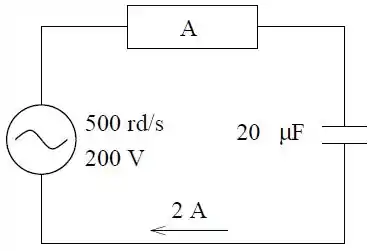
- Determine a potência média fornecida pelo gerador e a tensão eficaz no capacitor;
- Faça um diagrama indicando claramente os Fasores das tensões e da corrente. Determine a tensão eficaz no dispositivo e a sua defasagem em relação à corrente;
- Escreva a expressão da tensão no capacitor em função do tempo (adote fase inicial nula para a corrente);
Dado: .
Ver solução completaQuestão 30
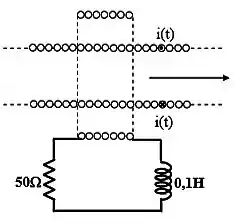
Num solenoide infinito passa uma corrente da forma . Ela possui e seu raio é de . Uma bobina de espiras e raio é colocada de tal forma que seus eixos de simetria coincidem. Aos extremos da bobina é acoplado um resistor e um indutor conforme a figura (a indutância da bobina é desprezível).
- Calcule a força eletromotriz sobre a bobina.
- Calcule a corrente máxima que passa pelo circuito e o ângulo de fase entre a e a corrente.
- Se colocarmos um capacitor no circuito, qual tem que ser o seu valor para que ele entre em ressonância?
Questão 33
O circuito elétrico de uma fábrica por ser representado, basicamente, pelo circuito da figura . As máquinas, que tem motores feitos de bobinas e também consomem energia, são representadas por elementos indutivos e resistivos. Em uma determinada fábrica, a fonte de corrente alternada possui uma amplitude de e uma frequência de ciclos de . A resistência equivalente de todas as máquinas é de e sua indutância equivalente é .
Obs.: Note que é zero nesse circuito.
- Calcule a amplitude de corrente e a diferença de fase entre a corrente e a tensão da fonte.
- Obtenha a potência média fornecida pela fonte e a potência média dissipada na resistência.
- Para ter eficiência máxima, qual deve ser o valor da capacitância do capacitor da figura ?
A operadora disponibiliza para fábrica uma potência média dada por . Para que a potência consumida pela fábrica (na resistência) tenha maior eficiência possível, isto é, seja a mesma fornecida pela operadora, instalam-se capacitores na sua linha, como mostrado na figura através de um capacitor equivalente.
Questão 34
Um circuito RLC tem voltagem de pico e corrente de pico . Se a corrente está atrasada em relação a tensão da fonte em , qual a potência média fornecida pela fonte ao circuito?
Questão 35
Uma fonte de corrente alternada com voltagem está em série com um resistor de e um capacitor cuja reatância, à frequência da fonte CA, é . A voltagem rms através do capacitor é:
Questão 36
Na figura abaixo, qual dos diagramas de fasores representa um circuito RLC em série com característica capacitiva?
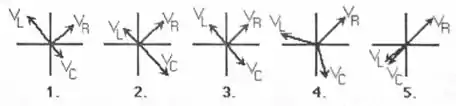
- 1
- 2
- 3
- 4
- 5
Questão 37
A impedância de um circuito em série certamente aumentará se:
- aumentar;
- diminuir;
- aumentar;
- diminuir;
- diminuir.
Questão 39
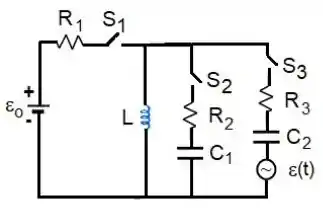
Muito tempo após o fechamento da chave , ela é aberta e, simultaneamente, apenas a chave é fechada, dando início à FASE 3 (a chave continua aberta). Nos itens seguintes, suponha que .
e) Desenhe o diagrama fasorial correspondente ao circuito relevante em escala, apresentando os valores dos fasores . Indique se o circuito é indutivo, capacitivo ou ressonante. Justifique sua resposta. Calcule o ângulo de fase entre e
Questão 40
Considere um circuito ideal constituído apenas por um indutor (indutância ) e um capacitor (capacitância ) em série. O gráfico de fasores que melhor descreve a corrente e as ddps no circuito é:
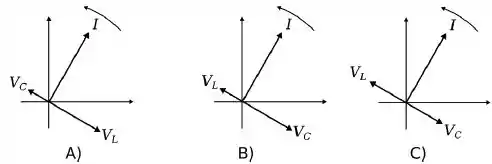
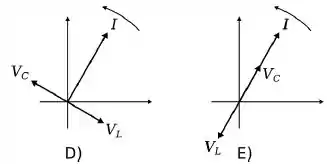
Questão 41
Em um circuito RLC, quando as reatâncias capacitiva e indutiva são iguais,
(a) A resistência é igual a zero
(b) O ângulo de fase é igual a zero
(c) A corrente elétrica se anula
(d) A fase é igual a radianos
(e) A tensão se anula
Ver solução completaQuestão 42
Um circuito em série consiste de uma fem com frequência angular de , um resistor de , um indutor de e um capacitor de . A corrente rms medida no circuito é de . Qual o fator de potência do circuito?
Ver solução completa
Questão 43
Qual a afirmativa correta quando num circuito a fem está em ressonância em em série?
A impedância tem seu valor máximo.
A reatância do indutor é nula.
A reatância do capacitor é nula.
A reatância devido ao indutor e o capacitor tem seu valor máximo.
A amplitude da corrente é máxima.
Ver solução completaQuestão 44
Quando um circuito RLC, em série, de corrente alternada está em ressonância, qual das alternativas a seguir é correta?
- A impedância tem seu valor máximo.
- A reatância do indutor é zero.
- A reatância do capacitor é zero.
- O ângulo de fase entre a fem e a corrente vale graus.
- A amplitude da corrente é máxima.
Questão 45
. Considere um circuito em série que tem uma capacitância e uma indutância . No momento inicial, , o capacitor possui carga nula, mas está sendo carregado por uma corrente .
Supondo uma solução do tipo , encontre , e .
Qual é o período de oscilação deste sistema.
Obtenha e esboce um gráfico das funções das energias elétrica (, no capacitor) e magnética (, no indutor), em função do tempo. Indique claramente os seus valores máximos e a escala de tempo.
Se colocarmos uma fonte de tensão alternada forçando este sistema, dada por , para qual valor de a corrente do circuito será máxima.
Ver solução completaQuestão 46
Uma fábrica comprou um novo motor para um de seus equipamentos. O motor é indutivo e funciona com corrente alternada, consumindo uma potência de (medido com um wattímetro) quando o motor está ligado a plena carga em uma rede de de tensão e de frequência. Com o motor ligado, foi medida uma corrente de . Com essas informações e sabendo que o motor é uma carga indutiva, responda: Qual é o fator de potência atual da instalação?
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 47
Um resistor e um capacitor são ligados em série com uma fonte de tensão alternada. Medidas de tensão feitas separadamente através do resistor e do capacitor dão os valores de e , respectivamente. Qual é aproximadamente a tensão () da fonte?
Questão 48
Um indutor ideal, de indutância desconhecida não nula, um resistor de resistência e um capacitor ajustável conectados em série a uma fonte de tensão alternada . A amplitude da corrente circulando no circuito quando o capacitor é ajustado para o valor é a mesma de quando o capacitor é ajustado para o valor .
Determine em função dos parâmetros dados:
(a) A indutância do indutor
(b) A amplitude da corrente no circuito
(c) A fase em relação à fonte de tensão quando o capacitor vale e
(d) A potência média dissipada no circuito qunado o capacitor vale
Ver solução completaQuestão 49
Se a frequência no circuito da figura aumentar, mantendo a amplitude da fonte constante, a corrente através do resistor
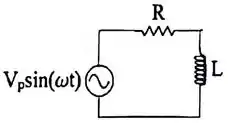
- Aumentará
- Diminuirá
- Não se altera
- Poderá aumentar ou diminuir, dependendo do valor original da frequência
- Poderá aumentar ou diminuir, dependendo dos valores de e de
Questão 50
Considere o circuito em corrente alternada mostrado em figura.
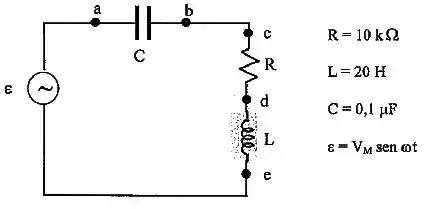
Sabendo que o valor máximo da tensão medida no capacitor (entre os pontos "a" e "b") é e que a frequência angular do gerador é :
Calcule o valor máximo da tensão entre os pontos “c” e “d” do circuito;
Calcule o valor máximo da tensão entre os pontos “d” e “e” do circuito;
Chamando , e , respectivamente, as tensões máximas no resistor, no capacitor e no indutor, desenhe (em escala) o diagrama dos fasores do circuito, indicando claramente , , e a corrente máxima .
Utilizando o diagrama, calcule a fase entre a tensão do gerador e a corrente que passa no circuito e o valor máximo da tensão do gerador, . Neste caso, o circuito possui comportamento indutivo ou capacitivo? Justifique a sua afirmação.
O circuito encontra-se em ressonância? Se sim, explique porque. Se não, calcule o valor do capacitor ou o indutor para que isso aconteça, mantida a frequência angular do gerador .
Ver solução completaQuestão 51
A figura mostra os fasores , e da f.e.m. do gerador de um circuito RLC em série, onde . O valor da f.e.m. instantânea é, respectivamente:
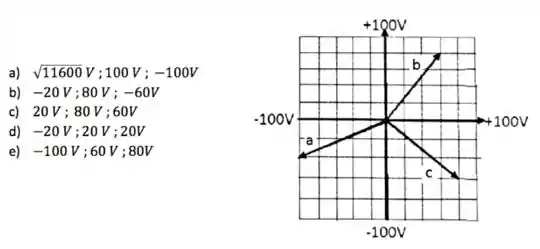
Questão 52
Um circuito ligado a uma fonte de corrente alternada é mostrado na Figura abaixo. Este circuito se encontra em ressonância e apresenta uma voltagem eficaz (rms) de .
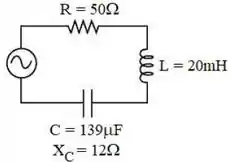
1) Qual é o valor da frequência de oscilação do gerador de corrente alternada que está ligado ao circuito?
(a)
(b)
(c)
(d)
(e)
2) Qual é o valor da impedância deste circuito?
(a)
(b)
(c)
(d)
(e)
3) Qual é o valor da corrente máxima que circula neste circuito?
(a)
(b)
(c)
(d)
(e)
4) O circuito da figura apresenta características:
(a) resistivas, pois os valores para as reatâncias indutiva e capacitiva são iguais.
(b) indutivas, pois a reatância indutiva apresenta um valor maior que a reatância capacitiva.
(c) indutivas, pois a constante de fase é positiva.
(d) capacitivas, pois a reatância indutiva apresenta um valor menor que a reatância capacitiva.
(e) capacitivas, pois a constante de fase é negativa.
5) Qual dentre os diagramas de fasores apresentados abaixo melhor representa a relação entre os fasores para a voltagem em cada elemento do circuito?
(a) 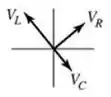
(b) 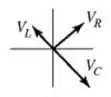
(c) 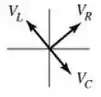
(d) 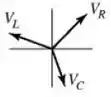
(e) 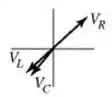
Questão 53
Uma corrente alternada é fornecida a um componente eletrônico cuja especificação afirma que ele deve ser usado apenas com voltagens abaixo de . Dentre os valores abaixo, qual a maior voltagem eficaz que pode ser aplicada a este componente de maneira que a voltagem limite não seja ultrapassada?
(a)
(b)
(c) .
(d)
(e)
Ver solução completaQuestão 54
Uma bobina formada por um conjunto de espiras de lados e está imersa em um campo magnético de . Ela pode ser girada através de uma manivela que se encontra fixa às suas extremidades. Esta manivela possui um mecanismo que só permite que ela gire em uma direção tal que a parte superior da bobina sempre está entrando na página, como mostra a figura.
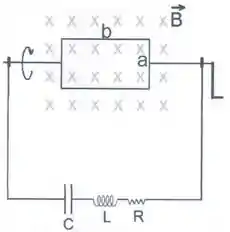
5) Sabendo que a bobina parte do repouso com seu plano perpendicular à página, como mostra a figura, ache a expressão para a força eletromotriz em função do tempo sabendo que a frequência angular da bobina é de .
(a)
(b)
(c)
(d)
(e)
Esta bobina é ligada então a um circuito em série, onde , e , como mostra a figura.
6) O circuito da figura tem características:
(a) resistivas, pois a voltagem do circuito está em fase com a corrente.
(b) indutivas, pois a voltagem do circuito está adiantada em relação à corrente.
(c) indutivas, pois a voltagem do circuito está atrasada em relação à corrente.
(d) capacitivas, pois a voltagem do circuito está adiantada em relação à corrente.
(e) capacitivas, pois a voltagem do circuito está atrasada em relação à corrente.
Ver solução completaQuestão 55
Uma linha de transmissão sem perdas é submetida a uma tensão dada por , onde é o tempo em segundos. Um indutor de em série e um resistor de em paralelo são introduzidos na linha (ver figura). Qual é o valor da tensão recebida na outra extremidade da linha?
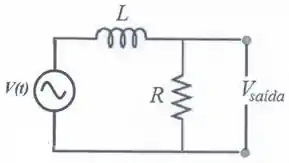
(a)
(b) .
(c)
(d)
(e)
Ver solução completaQuestão 56
No circuito da figura, , , e . Determine o valor da impedância do circuito.
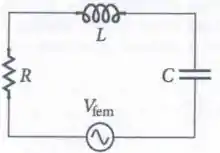
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 57
Um gerador AC produz (rms) a uma frequência de . Ele é ligado em série a um resistor com e um indutor com . A corrente rms é:
(a) e adiantada de em relação à fem.
(b) e atrasada de em relação à fem.
(c) e atrasada de em relação à fem.
(d) e atrasada de em relação à fem.
(e) e adiantada de em relação à fem.
Ver solução completaQuestão 58
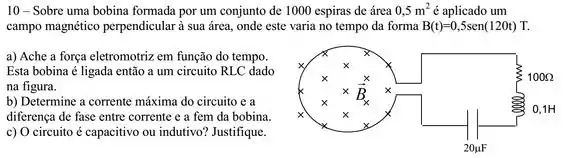
Sobre uma bobina formada por um conjunto de espiras de área é aplicado um campo magnético uniforme perpendicular à sua área, onde este varia no tempo do forma . Esta bobina é ligada, então, a um circuito RLC dado na figura.
A corrente máxima do circuito vale:
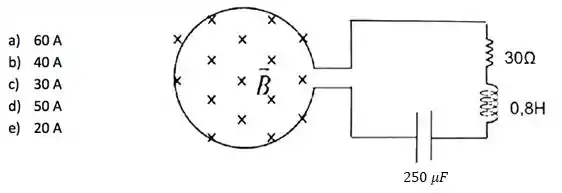
Questão 59
Um circuito de corrente alternada é constituído de uma indutância de em série com uma resistência de e alimentados por uma fonte de .
Qual o fator de potência do circuito;
Qual deve ser a capacidade de um capacitor que colocado em série com o circuito tornaria este fator de potência unitário?
De quando aumenta percentualmente a corrente no circuito com a introdução deste capacitor?
Qual a tensão no capacitor em função do tempo?
Qual a tensão medida por um voltímetro C.A. ligado no capacitor? E no indutor?
Ver solução completaQuestão 60
Considere um circuito RLC em série operando na condição de ressonância. Nessa situação a corrente através do circuito tem amplitude . Calcule:
- A impedância do circuito;
- A amplitude de voltagem da fonte ;
- As amplitudes de tensão no resistor , no capacitor e no indutor ;
- Dobra-se a frequência da fonte. Nessa nova situação, a potência média fornecida pela fonte aumenta, diminui ou permanece constante? Justifique.
Questão 61
A figura mostra os fasores para três circuitos RLC em série com uma fem senoidal de frequência . A alternativa correta que estabelece a relação entre e (frequência de ressonância) em cada circuito é:
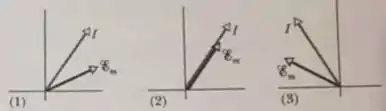
- Circuito (1): ; Circuito (2): ; Circuito (3): ;
- Circuito (1): ; Circuito (2): ; Circuito (3): ;
- Circuito (1): ; Circuito (2): ; Circuito (3): ;
- Circuito (1): ; Circuito (2): ; Circuito (3): ;
- Circuito (1): ; Circuito (2): ; Circuito (3): ;
Questão 62
Em um circuito RLC, a reatância capacitiva possui metade do valor da reatância indutiva e o ângulo de fase vale . Assumindo que conhecemos os valores da resistência e da indutância , podemos afirmar que a frequência angular vale:
Questão 63
Considere um circuito RLC em série com resistência e voltagem de pico de . Considerando que a corrente está atrasada de em relação à fem, a corrente rms no circtuito será de:
Questão 64
Uma fábrica brasileira iniciou a produção de um novo secador de cabelo. Seus secadores são montados com uma base para o motor do soprador e uma resistência frontal usada para aquecer o ar que está sendo soprado. Sendo assim, podemos modelar o secador como sendo um circuito RL ligado a uma fonte CA. Segundo as especificações da fábrica, o secador, quando ligado a uma rede de de tensão e de frequência, consome uma potência de . Um consumidor resolveu testar a eficiência deste soprador calculando o seu fator de potência. Para isso, ele mediu a corrente que estava sendo consumida com um amperímetro e obteve . Qual foi o valor encontrado para o fator de potência?
Questão 65
Em um circuito RLC em série de frequência angular , com resistência , um indutor de e um capacitor de , mede-se uma corrente de pico de . Após um período completo de oscilação a energia dissipada em cada componente do circuito será:
- , e
- ,
- , e
Questão 66
Um resistor, um indutor e um capacitor estão ligados em série com uma fonte de tensão . Qual das afirmações abaixo a respeito desse circuito é FALSA?
- A corrente é a mesma em todos os componentes em todos os componentes do circuito;
- Em qualquer instante, a soma das quedas de tensão em todos os elementos do circuito é igual a ;
- A corrente em pelo menos um dos componentes do circuito é dada por ;
- A tensão em pelo menos um dos componentes está defasada da tensão em outros componentes;
- A impedância do circuito é dada pela raiz quadrada de .
Questão 67
Um gerador produz a uma frequência de . Ele é ligado em série a um resistor com e um indutor com . A corrente é:
- e adiantada de em relação à ;
- e atrasada de em relação à ;
- e atrasada de em relação à ;
- e atrasada de em relação à ;
- e adiantada de em relação à ;
Questão 68
Uma fonte alternada com frequência angular e amplitude é ligada a um circuito em série que contém um capacitor, um indutor de indutância e um resistor de resistência .
- Para qual valor da reatância capacitiva a amplitude de voltagem através do indutor será máxima?
- O valor da capacitância do capacitor;
- A amplitude de voltagem através do indutor;
- O valor correspondente da amplitude de voltagem através do capacitor;
- O valor correspondente da amplitude de voltagem através do resistor.
Nas condições do item a) determine em função de , , e :
Questão 69
Um resistor de resistência , uma fonte de CA de fem de pico e frequência angular de e um indutor são acoplados em série. Para que a corrente de pico seja de , quanto deve valer a indutância do indutor utilizado?
Ver solução completa
Questão 70
No circuito abaixo, a tensão do gerador é , a amplitude da corrente é e a reatância indutiva é . O circuito está na condição de ressonância.
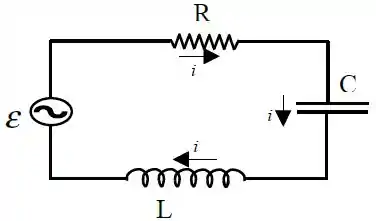
Qual é a impedância do circuito?
Qual é a resistência do resistor?
Calcule a sobre o capacitor e sobre o indutor em função do tempo;
Qual é a potência média dissipada no resistor?
Ver solução completaQuestão 71
No circuito mostrado na figura abaio, a corrente é dada por e a fonte de é . A reatância capacitiva deste circuito é .
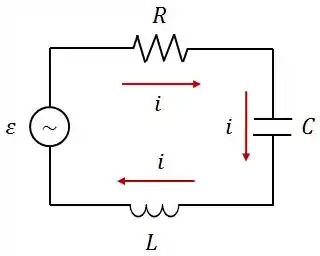
- Qual a impedância do circuito?
- Qual o valor da indutância?
- Qual é a constante de fase ?
- Qual a potência média dissipada no resistor?
- Para qual frequência da fonte a potência média dissipada em será máxima? Especificar.
Dados: , , e .
Ver solução completaQuestão 72
No circuito abaixo, a corrente é dada por e a fonte de é . A reatância capacitiva deste circuito é .
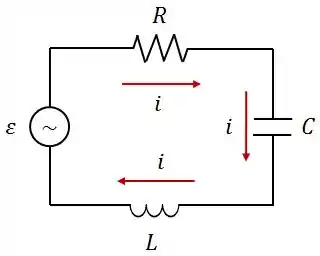
Dados: , , e , calcule:
A impedância do circuito;
O valor da indutância;
A constante de fase ;
A potência média dissipada nos resistor;
A frequência da fonte para a qual a potência média dissipada em será máxima;
Ver solução completaQuestão 73
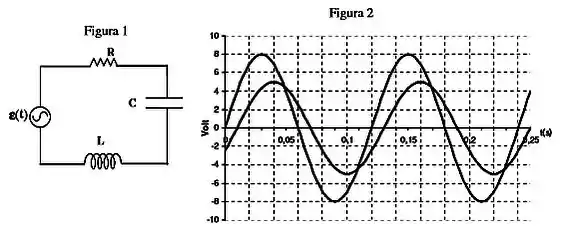
Um resistor, um indutor e um capacitor são conectados em série a uma fonte de corrente alternada (veja fig. ). No gráfico da figura , apresentamos as diferenças de potencial nas extremidades do resistor () e da fonte () em função do tempo.
- Determine, através do gráfico, os valores máximos de e de .
- Determine, através do gráfico, a frequência da fonte () e a diferença de fase entre a corrente e a ddp da fonte.
- O circuito é indutivo ou capacitivo? Justifique sua resposta.
Questão 75
Depois de medir a autoindutância de uma bobina, você a desenrola e então enrola metade do comprimento do fio em outra bobina com o mesmo diâmetro e mesmo comprimento, mas com a metade do número de espiras. Com esta ação, a autoindutância:
- Reduz-se a da anterior
- É a mesma
- Dobra
- Reduz-se à metade da anterior
- Quadruplica
Questão 77
No circuito da figura abaixo, o gerador de corrente alternada tem o valor da tensão quadrática média igual a quando opera na frequência.
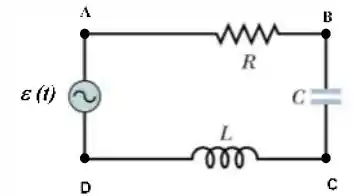
Sabendo que a indutância , a capacitância e que a resistência :
a) calcule os valores da tensão quadrática média entre os pontos: AB, BC e CD.
b) calcule os valores da tensão quadrática média entre os pontos: AC e BD.
c) Desenhe o diagrama de fasores do circuito indicando CLARAMENTE o valor de cada um deles. (Nota: cuidado para respeitar aproximadamente a escala entre os fasores).
d) Qual é o valor do ângulo de fase entre a corrente no circuito e a tensão do gerador?
e) Calcule o valor médio da potência fornecida pelo gerador.
Ver solução completaQuestão 78
Em um circuito LC contendo um indutor ideal de e um capacitor de , a carga máxima do capacitor é durante as oscilações. Qual é a corrente máxima através do indutor durante as oscilações?
Questão 79
Um circuito em série consiste de uma fem de frequência , um resistor de , um indutor de e um capacitor variável . A corrente rms medida no circuito é de .
A potência média fornecida pela fem será máxima quando:
A potência média dissipada no resistor for mínima.
A impedância for máxima.
A reatância capacitiva for maior do que a reatância indutiva.
O circuito entrar em ressonância.
O indutor receber metade da energia do capacitor.
Ver solução completaQuestão 80
No circuito abaixo a amplitude de voltagem da fonte é , o resistor é , a reatância capacitiva é e a reatância indutiva é .
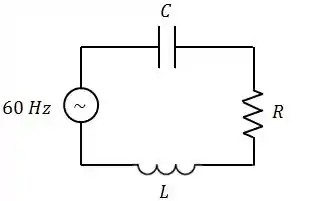
Qual a amplitude da corrente no circuito? Ela está atrasada ou adiantada em relação a fem?
, adiantada.
, atrasada.
, adiantada.
, atrasada.
, adiantada.
, atrasada.
Ver solução completaQuestão 81
No circuito em corrente alternada da figura, o capacitor é variável, com uma capacitância que pode ser regulada de zero até . O circuito é alimentado por uma fonte de tensão senoidal com valor máximo e frequência . Além disso, o resistor e o indutor possuem os seguintes valores: e .
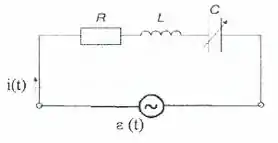
Nestas condições (nas contas, considere ):
(a) Calcule o valor da capacitância para que o fator de potência do circuito seja igual a . O circuito tem comportamento capacitivo ou indutivo? Justifique suas afirmações
(b) Calcule o valor máximo da corrente e as tensões no resistor , no capacitor e no indutor . Desenhe também o diagrama dos fasores (em escala).
(c) Qual valor deve ter para que o circuito entre em ressonância? Calcule nesta nova condição o valor médio da potência dissipada no resistor.
Ver solução completaQuestão 82
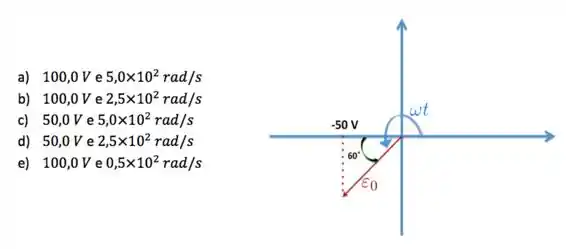
Considere que o diagrama abaixo descreva a voltagem de uma fonte CA no instante . Os valores de pico da fem e da frequência angular da fonte CA são, respectivamente,
Questão 83
Considere apenas um indutor conectado a um gerador CA de voltagem de pico de . Sabendo que a corrente de pico vale , determine a frequência e o valor instantâneo da ddp () no indutor no instante em que o valor da corrente é máxima
- e
- e
- e
- e
- e
Questão 84
Assinale a única alternativa que está incorreta.
- Quanto maior a impedância de um circuito RLC, menor a corrente de pico
- A impedância de um circuito RLC sempre cresce se aumentarmos a resistência
- Quanto mais próximos os valores da reatância capacitiva e da reatância indutiva, mais próximos do fenômeno de ressonância estaremos
- A impedância será nula quando o sistema estiver em ressonância
- A impedância de um circuito RLC não depende do valor de pico da fonte
Questão 85
Considere o circuito abaixo. Um resistor , um capacitor e um indutor são ligados em paralelo a uma fonte de tensão alternada. Qual(is) das seguintes afirmações é(são) correta(s)?
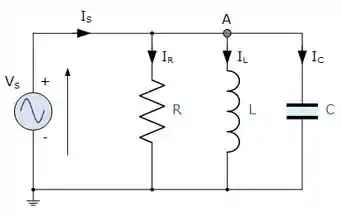
I. A soma das correntes instantâneas em cada elemento deve ser igual à corrente instantânea fornecida pela fonte.
II. A soma das voltagens instantâneas através de cada elemento deve ser igual à voltagem da fonte;
III. A voltagem instantânea através de está defasada de em relação à voltagem através de .
IV. A voltagem instantânea através de está defasada de em relação à voltagem através de .
V. Toda a energia é dissipada pelo resistor.
(a) somente II, IV e V são corretas.
(b) somente II e V são corretas.
(c) somente I, III e V são corretas.
(d) somente I, IV e V são corretas.
(e) somente I e V são corretas.
Ver solução completaQuestão 86
Um gerador de com e operando a provoca oscilações em um circuito em série que possui , e . Determine:
c) a fase da corrente
d)o fator de potência
Ver solução completaQuestão 88
Uma fonte de corrente alternada está conectada a um resistor com , um indutor com e um capacitor com . Qual a diferença de fase entre a voltagem da fonte e a corrente no circuito quando a frequência da fonte for igual a ?
(a)
(b) .
(c) .
(d) .
(e) .
Ver solução completaQuestão 89
Um capacitor de capacitância foi ligado em série com um resistor de e um gerador de corrente alternada que imprime uma tensão variável neste circuito dada por . Determine a função que descreve a forma com que a corrente de deslocamento está variando com o tempo entre as placas do capacitor.
(a)
(b) onde .
(c)
(d)
(e) onde .
Ver solução completaQuestão 90
Em um circuito CA genérico, a amplitude da corrente que passa por um dado resistor foi medida e vale . A ddp neste mesmo resistor também foi medida (usando-se um osciloscópio): a amplitude da onda observada vale e o período da onda vale .
A expressão para a corrente que atravessa o resistor e sua ddp em função do tempo são representadas pelas funções:
e
e
e
e
e
Ver solução completaQuestão 91
Um motor elétrico conectado a uma tomada elétrica de e executa um trabalho mecânico a uma taxa de (). Se este motor drena uma corrente rms de , qual é o valor do seu fator de potência?
(a)
(b) .
(c) .
(d) .
(e) .
Ver solução completaQuestão 92
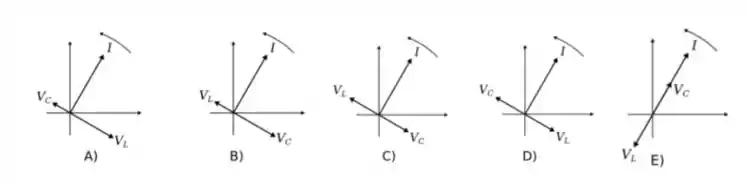
Considere um circuito ideal () constituído apenas por um indutor (indutância ) e um capacitor (capacitância ) em série. O gráfico de fasores que melhor descreve a corrente e as ddps do circuito na situação de ressonância é:
Questão 93
A diferença de potencial sobre um indutor em um circuito RLC em série:
- Pode ser maior que a amplitude máxima da f.e.m do gerador de corrente alternada.
- É sempre menor que a amplitude máxima da f.e.m. do gerador de corrente alternada.
- É no máximo igual à amplitude máxima da f.e.m. do gerador de corrente alternada.
- É no mínimo igual à amplitude máxima da f.e.m. do gerador de corrente alternada.
- É sempre igual à amplitude máxima da f.e.m. do gerador de corrente alternada.
Questão 95
Num circuito em série, a frequência de ressonância é . Se dobrarmos os valores da resistência, da indutância, da capacitância e da amplitude da fonte de voltagem , qual será a nova frequência de ressonância?
Ver solução completa
Questão 97
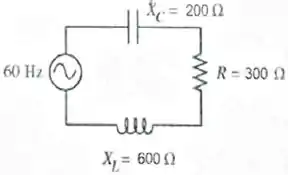
Uma fonte CA (de corrente alternada) de frequência em um circuito RLC em série tem amplitude de voltagem de . A resistência, a reatância capacitiva e a reatância indutiva tem os valores mostrados na figura. Qual é o valor da amplitude de corrente no circuito?
Questão 98
Um circuito RLC de corrente alternada em série possui frequência de ressonância e impedância . O pico da fonte é ajustada em e a corrente de pico vale . (a) Escreva uma relação entre e como função dos dados. (b) Supondo que , determine e
Ver solução completaQuestão 99
Qual dos diagramas de fasores mostrados abaixo representa um circuito em série em ressonância?
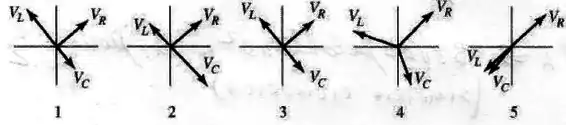
1
2
3
4
5
Ver solução completaQuestão 101
No circuito de corrente alternada abaixo sabe-se que o valor quadrático médio da diferença de potencial . Além disso, sabe-se que a amplitude da d.d.p entre os pontos e é dada por: .
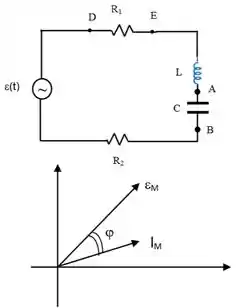
São conhecidos também os valores dos seguintes componentes:
Considerando o diagrama de fasores do circuito e sabendo que escreva a expressão de .
Determine o valor da capacitância .
Determine o valor do resistor .
Pelo gráfico dos fasores o circuito não está em ressonância. Para que isso aconteça é preciso aumentar ou diminuir o valor de ? Justifique as suas afirmações.
Uma vez estabelecida a ressonância no circuito, qual serão os novos valores das amplitudes de e ?
Ver solução completaQuestão 102
Em um circuito RLC em série, os valores das voltagens instantâneas em um certo instante de tempo são: , e . Com estas informações, o valor da voltagem da fonte neste momento é:
Questão 103
Um circuito RLC em série é alimentado por uma fonte CA com frequência duas vezes maior que a frequência de ressonância. Sobre as reatâncias do sistema, podemos afirmar que:
.
.
.
.
.
Ver solução completaQuestão 104
A figura mostra um filtro passa-alta, composto de um resistor de resistência , um indutor de indutância e um capacitor de capacitância , que permite a passagem de frequências altas com facilidade, porém atenua (ou reduz) a amplitude das frequências abaixo de uma frequência de corte. A amplitude da tensão de entrada é e a amplitude da tensão de saída é , que é medida nos extremos do indutor. Calcule, em função da frequência angular da fonte:
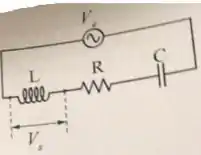
a) A amplitude da corrente que circula no circuito.
b) A amplitude da tensão de saída .
c) A relação entre as amplitudes, ou seja, .
d) Calcule o limite da razão para .
Ver solução completaQuestão 105
9 - Qual dos diagramas de fasores mostrados abaixo melhor representa um circuito LRC em série na situação de ressonância?
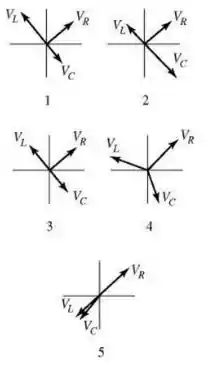
Questão 107
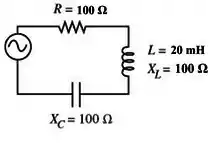
Em um circuito RLC em série com , e , que valor aproximado de frequência a fonte deve ter para minimizar a impedância?
Questão 108
Dadas as seguintes afirmações:
- Em um circuito RLC, se a resistência é dobrada, a frequência de ressonância cai pela metade;
- Em ressonância, a impedância de um circuito RLC é igual a R;
- Em ressonância, a corrente de um circuito RLC está em fase com a fonte de CA;
- Perto da ressonância, o fator de potência de um circuito RLC é próximo de zero;
Quais das alternativas abaixo contém todas as afirmativas verdadeiras?
- II, IV
- I, IV
- II, III
- III, IV
- I, III
Questão 109
Considere o circuito de corrente alternada da figura 1, onde a frequência angular da fonte é. A posição relativa dos fasores da fonte e da corrente é mostrada na figura 2. Com a adição de um indutor em série , a posição relativa dos fasores muda para a da figura 3.
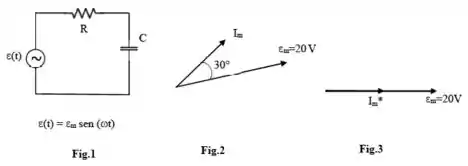
Determine, justificando todas as respostas:
- O valor da capacitância .
- A amplitude da corrente na ausência da indutância .
- O valor da resistência .
- A potência média fornecida pela fonte sem a indutância
- A potência média fornecida pela fonte com a indutância .
- A potência média absorvida pelo resistor sem e com a indutância .
Questão 110
Um motor ligado a uma linha de força de (valor rms)/ usa de potência média a um fator de potência igual a . Considere que o motor é um circuito RLC sem o capacitor (). Qual é a corrente rms no motor?