Exercícios de Momento Magnético Dipolar - Lista de Exercícios Resolvida
Questão 1
Uma bússola encontra-se acima de um fio retilíneo, muito longo, percorrido por uma corrente elétrica estacionária de intensidade . Na sua posição de equilíbrio estável, quais são o sentido do vetor momento de dipolo magnético da bússola e a sua energia potencial , supondo que esta última é zero quando .
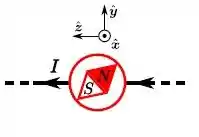
- e
- e
- e
- e
- e
- e
Questão 2
Um elétron se move em um círculo de raio com uma velocidade de .
Trate a trajetória circular como uma espira de corrente igual à razão entre a carga do elétron e o período do movimento.
Se a trajetória do elétron está em uma região onde existe um campo magnético uniforme de módulo , qual é o maior valor possível do módulo do torque aplicado pelo campo à espira?
Ver solução completaQuestão 3
Um fio condutor, curvado na forma de um semicírculo de raio , forma um circuito fechado e é percorrido por uma corrente . O circuito está no plano e um campo magnético uniforme está aplicado paralelamente ao eixo , com é visto na figura.
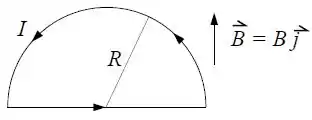
Determine a força magnética total (vetor) sobre a parte retilínea do condutor.
Determine a força magnética total (vetor) sobre a parte curva do condutor.
Determine o vetor torque exercido por sobre o circuito.
Ver solução completaQuestão 4
A bobina da figura conduz uma corrente no sentido indicado, é paralela ao plano , tem espiras, tem uma área de e está submetida a um campo magnético uniforme .
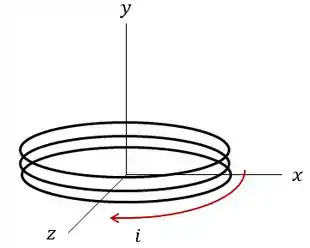
Determine:
- A energia potencial magnética do sistema bobina-campo magnético;
- O torque magnético (na notação de vetores unitários) a que está sujeita a bobina;
Questão 5
A figura abaixo mostra uma bobina retangular de cobre, de 20 espiras, com de altura e de largura.
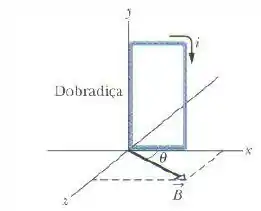
A bobina conduz uma corrente de e dispões de uma dobradiça em um dos lados verticais. Ela está montada no plano , fazendo um ângulo de com a direção de um campo magnético uniforme de módulo .
Em termos dos vetores unitários, qual é o torque que o campo exerce sobre a bobina em relação à dobradiça?
Ver solução completaQuestão 6
Uma espira circular com de raio é percorrida por uma corrente de .
Um vetor de comprimento unitário, paralelo ao momento dipolar da espira é dado por . Se a espira é submetida a um campo magnético uniforme dado por
Determine o torque sobre a espira (em termos dos vetores unitários) e a energia potencial magnética da espira.
Ver solução completaQuestão 7
Duas espiras circulares concêntricas, de raios e , estão situadas no plano . Ambas são percorridas por uma corrente no sentido horário, conforme a figura abaixo.
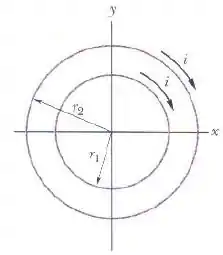
Determine o módulo do momento dipolar magnético do sistema.
Repita o cálculo supondo que a corrente da espira menor mudou de sentido.
Ver solução completaQuestão 8
O módulo de momento dipolar magnético da Terra é . Suponha que esse momento é produzido por cargas que circulam na parte externa do núcleo da Terra. Se o raio da trajetória dessas cargas é , calcule a corrente associada.
Ver solução completaQuestão 9
Uma bússola encontra-se acima de um fio retilíneo, muito longo, percorrido por uma corrente elétrica estacionária de intensidade . Na sua posição de equilíbrio estável, quais são o sentido do vetor momento de dipolo magnético da bússola e a sua energia potencial , supondo que esta última é zero quando .
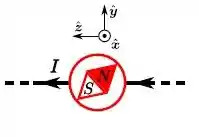
- e
- e
- e
- e
- e
- e
Questão 10
Com base na figura, responda:

Qual o módulo do torque sobre a espira?
Qual é a orientação de equilíbrio da espira?
Ver solução completaQuestão 11
Os diagramas abaixo mostram cinco possíveis orientações de um dipolo magnético em um campo magnético uniforme . Para qual destes o torque magnético sob o dipolo tem a sua maior intensidade?
(a) I
(b) III
(c) V
(d) IV
(e) II
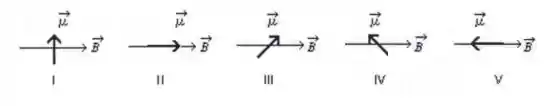
Questão 12
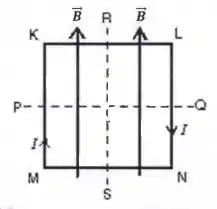
Uma espira quadrada situa-se no plano da página e transporta uma corrente , como mostra a figura. Existe um campo magnético uniforme paralelo ao lado como indicado. A espira tende a girar no:
(a) entorno de com saindo da página.
(b) entorno de com entrando para a página.
(c) entorno de com saindo da página.
(d) entorno de com entrando para a página.
(e) entorno de um eixo perpendicular à página.
Questão 13
. Considere a espira condutora mostrada na figura abaixo. Ela é formada pela junção de dois trechos semicirculares de raios e com dois trechos retilíneos e conduz uma corrente estacionária de intensidade no sentido indicado.
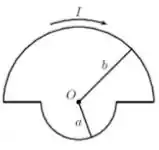
Determine o vetor momento de dipolo magnético da espira.
Ver solução completaQuestão 14
A espira retangular da figura abaixo está colocada no plano em um campo magnético:
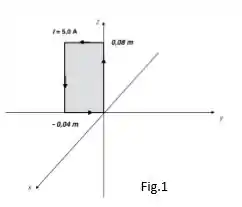
Na espira circula uma corrente com o sentido indicado na figura.
(a) Calcule o vetor momento magnético associado a essa espira.
(b) Calcule o vetor torque exercido pelo vetor campo magnético sobre a espira.
(c) Em seguida a espira é girada em torno do eixo no sentido anti-horário e colocada a (ver figura ). Calcule o vetor torque na espira nesta posição.
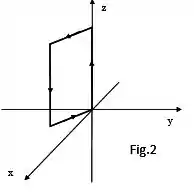
Questão 15
Uma espira condutora quadrada de lado é posicionada sobre o plano de um sistema de coordenadas, como mostrado na figura abaixo. Uma corrente estacionária de intensidade circula a espira no sentido indicado. Ela está imersa em uma região de campo magnético estacionário e uniforme dado por , onde é uma constante positiva. Nessa situação, o momento de dipolo magnético da espira e o torque magnético sobre ela valem, respectivamente:
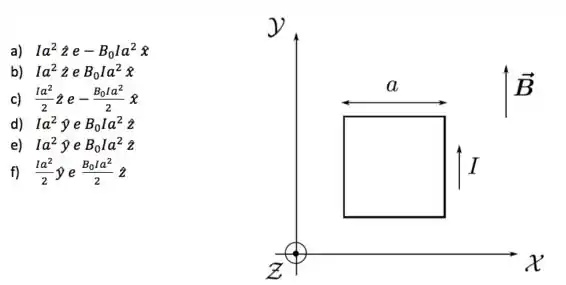
Questão 16
Um fio, transportando uma corrente , é dobrado de modo a formar uma espira semicircular de raio , conforme a figura.
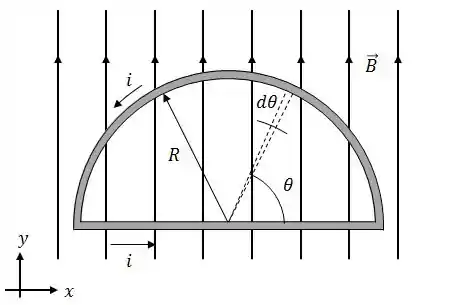
O fio está no plano e o vetor é dado por .
Calcule a força magnética que age sobre a parte reta do fio;
Calcule a força magnética que age sobre a parte curva do fio;
Calcule a força magnética total sobre a espira;
Calcule o vetor momento de dipolo magnético da espira;
Calcule o torque magnético sobre a espira;
Ver solução completaQuestão 17
Uma espira circular com de raio carrega uma corrente de . Ela é colocada em um campo magnético uniforme de magnitude que é direcionado paralelamente ao plano da espira, como sugerido na figura. Qual é a magnitude do torque exercido nesta pelo campo magnético?
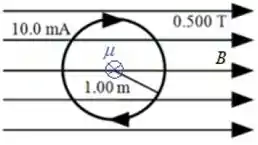
(a)
(b)
(c)
(d)
(e) zero
Ver solução completaQuestão 18
Uma espira triangular, de base e altura , contida no plano , é percorrida por uma corrente no sentido horário, conforme a figura abaixo. Na região onde se encontra a espira, existe um campo magnético
onde é uma constante.
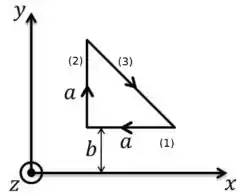
- Calcule o vetor força magnética sobre os lados 1 e 2 da espira.
- Calcule o vetor força magnética sobre o lado 3 da espira.
- Determine o vetor momento de dipolo magnético e o vetor força resultante sobre a espira.
Questão 19
Uma espira é formada por dois segmentos de reta de comprimento e um trecho semicircular de raio , conforme ilustrado na figura. A espira está sujeita a um campo magnético uniforme dado por e a corrente percorre a espira no sentido indicado na figura.
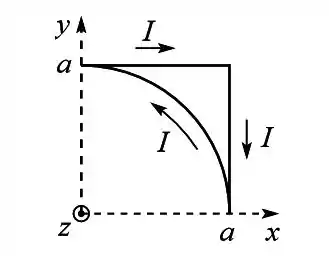
(c) Determine o torque da espira.
Ver solução completaQuestão 20
Uma espira condutora retangular de lados e é posicionada sobre um sistema de coordenadas como mostrado na figura abaixo. Um de seus lados está sobre o eixo e o seu plano forma um ângulo com o plano . Ela transporta uma corrente estacionária de intensidade , no sentido indicado, e encontra-se sob a ação de um campo magnético constante , também indicado na figura. Nessas condições, o torque que o campo magnético exerce sobre a espira vale:
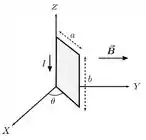
Questão 21
A figura ilustra uma espira circular de raio na qual circula uma corrente elétrica no sentido horário. A espira situa-se no plano e um campo magnético uniforme externo de magnitude aponta na direção positiva do eixo , como ilustrado.
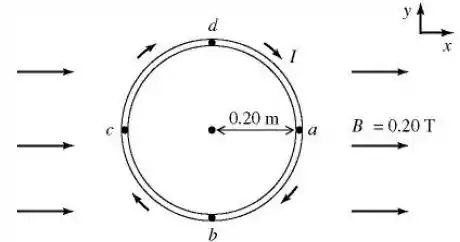
A magnitude do momento de dipolo magnético da espira é .
Qual a intensidade da corrente na espira?
Ver solução completa
Questão 22
15 - Considere três espiras circulares de raios e . Para que as três espiras tenham o mesmo valor de dipolo magnético, as correntes nas espiras devem ser, respectivamente,
Questão 23
Um fio, transportando uma corrente , é dobrado de modo a formar uma espira semicircular de raio , conforme a figura. O fio está no plano e o vetor é dado por .
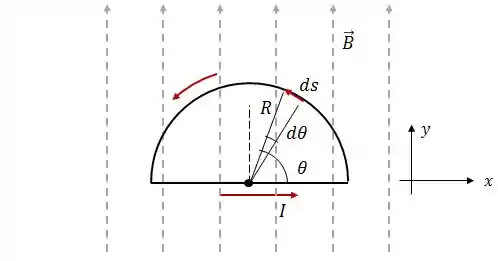
Calcule a força magnética que age sobre a parte reta do fio;
Calcule a força magnética que age sobre a parte curva do fio;
Calcule a força magnética que age sobre a espira;
Calcule o vetor momento de dipolo magnético da espira;
Calcule o torque magnético sobre a espira;
Ver solução completaQuestão 24
Ordene os módulos dos torques que agem nas espiras circulares , e que aparecem na figura, do maior para o menor. As três espiras são idênticas e transportam correntes iguais.
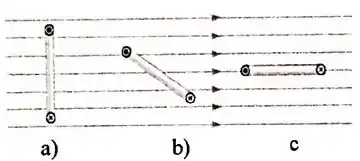
a, b, c;
a, c, b;
c, a, b;
c, b, a;
b, c, a;
Ver solução completaQuestão 25
(Capítulo 28.10 – Exercício 57) Uma bobina circular de 160 espiras tem um raio de 1,90 cm. (a) Calcule a corrente que resulta em um momento dipolar magnético de módulo . (b) Determine o valor máximo do torque a que a bobina é submetida quando, sendo percorrida por essa corrente, é colocada na presença de um campo magnético uniforme de módulo 35,0 mT.
Ver solução completaQuestão 26
Um dipolo magnético puntiforme, de momento de dipolo , está localizado na origem de um sistema de eixos cartesianos, como indicado na figura abaixo.
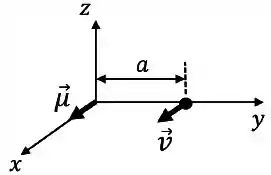
Em um dado instante, uma partícula de carga positiva tem vetor posição e velocidade , onde e são constantes positivas.
Podemos afirmar que, no instante em questão, a força magnética sobre a partícula:
tem sentido ;
tem sentido ;
tem sentido ;
tem sentido ;
tem sentido ;
tem sentido ;
é nula;
Ver solução completaQuestão 27
A figura mostra quatro orientações, definidas pelo ângulo , de um momento de dipolo magnético em um campo magnético .
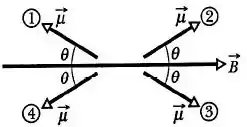
Ordene, começando pelo maior, o trabalho realizado por um agente externo sobre o dipolo para as três rotações seguintes: , e .
, e ;
, , ;
e empatados, ;
e empatados, ;
, , ;
Ver solução completaQuestão 28
Na figura abaixo o campo magnético é uniforme e perpendicular ao plano da figura, apontando para fora (direção positiva do eixo ). A espira é formada por um quarto de círculo de raio (arco ) e por dois segmentos retilíneos e de comprimento , conforme-te a figura. Pela espira circula uma corrente no sentido anti-horário.
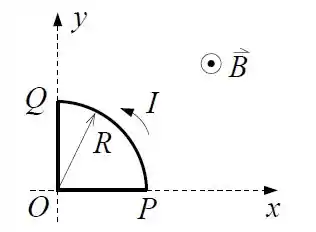
Calcule o torque que age sobre a espira.
Ver solução completaQuestão 29
A figura ilustra uma espira circular de raio na qual circula uma corrente elétrica no sentido horário. A espira situa-se no plano e um campo magnético uniforme externo de magnitude aponta na direção positiva do eixo , como ilustrado.
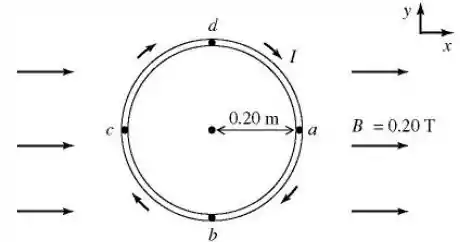
A magnitude do momento de dipolo magnético da espira é .
Se a espira for liberada, a partir do repouso, da configuração mostrada na figura, seu movimento devido ao torque magnético é tal que (considere os 4 pontos representados na espira, rotulados de a , b , c e d ):
a espira não se moverá, pois está em uma configuração de equilíbrio estável.
ponto a move-se para fora da página e ponto move-se para dentro da página.
ponto a move-se para dentro da página e ponto move-se para fora da página.
ponto b move-se para fora da página e ponto move-se para dentro da página.
ponto b move-se para dentro da página e ponto move-se para fora da página.
Ver solução completaQuestão 30
Considere uma espira quadrada de lado percorrida por uma corrente . A espira se encontra no plano , conforme a figura.
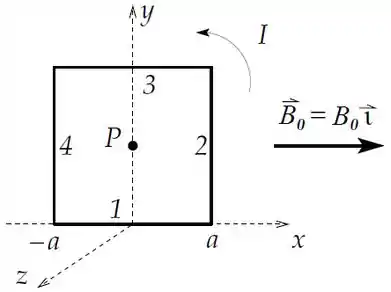
Determine o vetor torque que o campo externo exerce sobre a espira.
Ver solução completaQuestão 31
Um fio condutor, curvado na forma de um semicírculo de raio , forma um circuito fechado e é percorrido por uma corrente . O circuito está no plano e um campo magnético uniforme está aplicado paralelamente ao eixo , com é visto na figura.
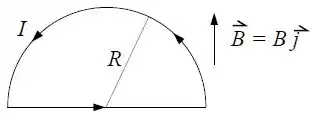
Determine o vetor torque exercido por sobre o circuito.
Ver solução completaQuestão 32
Uma bobina circular de área possui espiras e está livre para girar em torno do seu diâmetro que coincide com o eixo . Uma corrente está circulando na bobina que se encontra imersa a um campo magnético no sentido positivo de . O torque quando a bobina está orientada na posição indicada na figura abaixo são dados por:
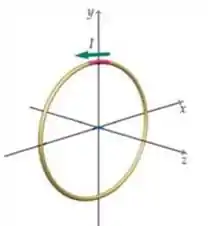
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 33
10 - Sobre campos magnéticos, marque a única alternativa alterna verdadeira.
- As linhas de campo magnético têm sua origem nas cargas magnéticas, conhecidas como monopólios magnéticos.
- Monopolos magnéticos existem em abundância na Natureza. Sem eles o que conhecemos por carga elétrica não existiria.
- Até o momento, não há evidência experimental da existência de monopolos magnéticos. As fontes mais básicas de campo magnético são os dipolos magnéticos.
- As linhas de campos magnético são sempre paralelas às correntes elétricas.
- Imãs permanentes produzem campos magnéticos, pois possuem monopolos magnéticos.
Questão 34
Uma corrente estacionária circula no sentido anti-horário de uma espira condutora quadrada, de lado . A figura ao lado mostra a espira em um sistema de coordenadas tal que o plano da espira coincide com o plano . Considere o campo magnético (no mesmo sistema de coordenadas)
- Calcule as forças magnéticas que atuam em cada um dos lados da espira (como indicados na figura). Calcule também a força resultante sobre a espira.
- Suponha que o movimento da espira seja restrito a rotações em torno de um eixo vertical fixo passando pelos pontos (veja a figura). Calcule o torque em torno deste eixo em relação à origem.
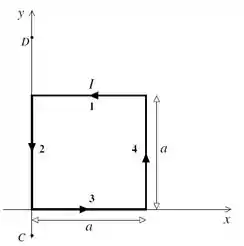
Sugestão para os itens e Calcule primeiramente as forças infinitesimais e em seguida obtenha , efetuando a integral correspondente.
Ver solução completaQuestão 35
15 - A figura ao lado mostra uma espira transportando uma corrente e o campo magnético produzido. Sobre esse sistema, podemos afirmar que:
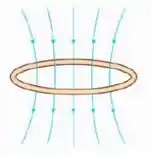
- O momento de dipolo está orientado para cima e o polo norte está abaixo da espira.
- O momento de dipolo está orientado para cima e o polo norte está acima da espira.
- É impossível resolver esta questão sem saber a orientação da corrente .
- O momento de dipolo está orientado para baixo e o polo norte está acima da espira.
- O momento de dipolo está orientado para baixo e o polo norte está abaixo da espira.
Questão 37
Um nêutron é formado por três partículas elementares conhecidas como quarks. Um deles é um quark up, com carga e os outros dois são quarks down, cada um com carga . Em um modelo simplificado para a estrutura interna do nêutron, os três quarks realizam movimentos circulares de mesma velocidade escalar e raio , todos executados no mesmo plano. O quark up gira em sentido anti-horário e os quarks down giram em sentido horário, como vistos por um mesmo observador. Nessas condições, supondo que as correntes elétricas associadas ao movimento de cada quark podem ser tratadas como correntes estacionárias, a intensidade do momento de dipolo magnético total do nêutron vale:
Questão 38
Uma espira quadrada, de arestas de comprimento , pela qual flui uma corrente estacionária de intensidade , está no plano , com dois de seus lados paralelos ao eixo , como mostrado na figura abaixo.
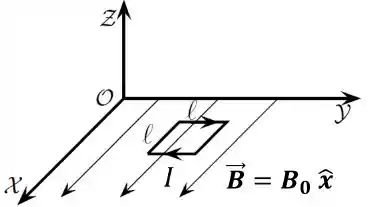
A corrente na espira flui no sentido horário para um observador localizado no semi-eixo positivo . Na região onde a espira se encontra há um campo magnético constante (estacionário e uniforme) .
O torque sobre a espira é dado por:
;
;
;
;
;
;
;
Nulo;
Ver solução completaQuestão 39
Na figura abaixo, uma espira de corrente, que tem a forma de um triângulo equilátero de lado , é percorrida por uma corrente elétrica no sentido indicado. Um campo magnético uniforme , que ocupa todo o espaço, é aplicado ao longo do eixo , como esquematicamente representado na figura. Considere que os vetores unitários ao longo dos eixos , e , são respectivamente representados por , e . Nestas condições, calcule:
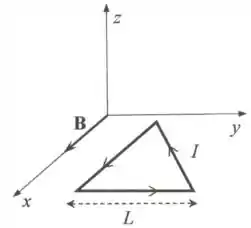
- O vetor momento de dipolo magnético da espira.
- O vetor torque que atua na espira.
- A diferença de energia potencial magnética , se a espira passar de sua posição inicial mostrada na figura acima (associada à ), para uma posição final (associada à ) em que seu momento de dipolo magnético for paralelo ao campo magnético aplicado . Observação: adote o nível de energia potencial magnética nula como aquele em que o vetor momento de dipolo magnético é perpendicular ao vetor .
