Exercícios de Oscilações Acopladas - Lista de Exercícios Resolvida
Questão 1
Uma cadeia linear de partículas de massa , ligadas com molas de constante elástica e massa desprezível, precisa de quantas condições iniciais para a completa descrição do sistema? Considere apenas deslocamentos longitudinais.
Questão 2
Dois pêndulos, cada um composto por um fio de comprimento prendendo uma partícula de massa , realizam um movimento harmônico simples (pequenas amplitudes) com uma mola de constante elástica e massa desprezível unindo as massas no plano de oscilação. Quais o modos normais de oscilação?
- e
- e
- e
- e
- e
Questão 3
Considere dois osciladores harmônicos idênticos com constantes de mola e acoplados por uma mola muito fraca com constante . A variação na frequência de vibração do modo antissimétrico com relação ao modo simétrico vale aproximadamente?
Dica: Usar a aproximação: , quando .
Ver solução completaQuestão 4
Considere um sistema formado por duas partículas idênticas de massa ligadas por uma mola de massa desprezível e constante elástica . Supondo que as partículas se movem em apenas uma direção e a única força atuante no sistema advém da mola, assinale a alternativa correta para a frequência angular de oscilação.
Questão 5
Dado um sistema de duas partículas de massa ligados por três molas de constante elástica e massa desprezível, como ilustrado abaixo:
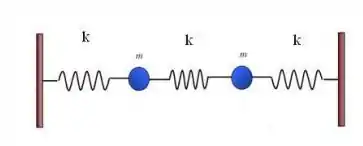
O sistema possui dois modos normais de vibração, e , onde . Quando o sistema oscila com frequência ou , a frequência de oscilação do centro de massa é respectivamente
- e
- e
- e
- e
- e
Questão 6
Dado um sistema de duas partículas de massa ligados por três molas de constante elástica e massa desprezível, como ilustrado abaixo:
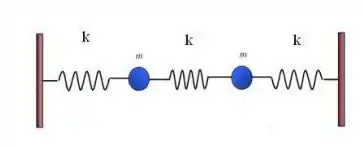
O sistema possui dois modos normais de vibração, e , onde . Quando o sistema oscila com frequência ou , a frequência de oscilação do centro de massa é respectivamente
- e
- e
- e
- e
- e
Questão 7
Considere um sistema formado por duas partículas idênticas de massa ligadas por uma mola de massa desprezível e constante elástica . Supondo que as partículas se movem em apenas uma direção e a única força atuante no sistema advém da mola, assinale a alternativa correta para a frequência angular de oscilação.
Questão 8
Dois sistemas massa mola encontram-se acoplados como mostra a figura. Sendo e a chamada razão áurea, o sistema tem dois modos normais com frequências e tais que:
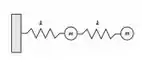
Observação: Existe um erro no enunciado: . O correto é . Além disso, não encontramos uma resposta que esteja listada acima.
Ver solução completaQuestão 9
As figuras (1), (2) e (3) mostram diferentes configurações de sistemas massa-mola. Todas as massas e molas das figuras são iguais. Em relação às frequências de oscilação, podemos afirmar que:

Questão 10
Uma plataforma de massa m está presa a duas molas iguais e de constantes elásticas k numa superfície horizontal sem atrito. Um bloco de massa M = 4m é colocado sobre a plataforma com as molas nas condições relaxadas, como mostrado na figura. Em função de k, m e M, responda:
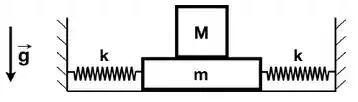
- Qual a frequência angular de oscilações dos blocos, quando estes são deslocados da posição de equilíbrio e liberados?
- Calcule a amplitude máxima de oscilação para que o bloco não deslize sobre a plataforma, sabendo que o coeficiente de atrito estático entre o bloco e a plataforma é .
- Soltando o bloco+plataforma de uma posição ( e com velocidade nula, determine a posição do sistema em função do tempo.
Questão 11
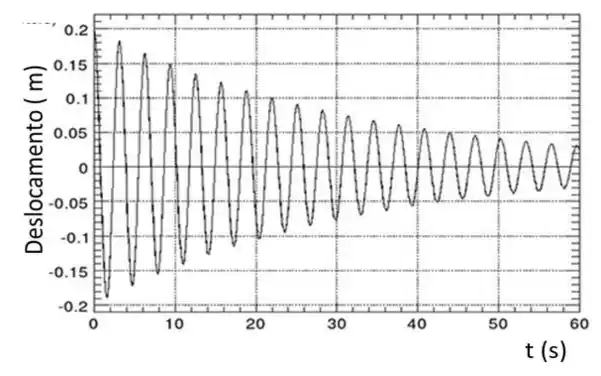
Através de uma força de , um oscilador harmônico amortecido é deslocado de da sua posição de equilíbrio. Em ele é solto (do repouso) e começa a oscilar. O movimento é então registrado como mostrado no gráfico abaixo. Faça uma estimativa, mais precisa que você conseguir, dos valores do período e da massa.
Questão 12
Considere dois osciladores harmônicos idênticos com constantes de mola e acoplados por uma mola muito fraca com constante . A variação na frequência de vibração do modo antissimétrico com relação ao modo simétrico vale aproximadamente?
Ver solução completaQuestão 13
Dois pêndulos, cada um composto por um fio de comprimento prendendo uma partícula de massa , realizam um movimento harmônico simples (pequenas amplitudes) com uma mola de constante elástica e massa desprezível unindo as massas no plano de oscilação. Quais o modos normais de oscilação?
- e
- e
- e
- e
- e