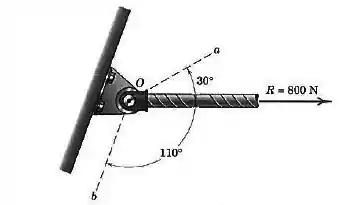
Determine os componentes retangulares e da força ao longo dos eixos não retangulares e . Determine também a projeção ortogonal de sobre o eixo .
Passo 1
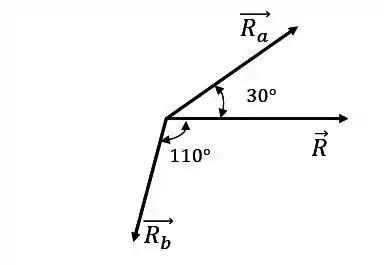
As componentes que queremos achar e a força podem ser vistas abaixo:
Passo 2
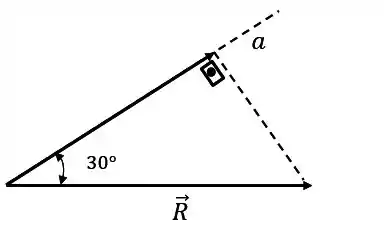
Se deslocarmos o vetor , sem mudar a sua direção e sentido, podemos formar o seguinte triângulo:
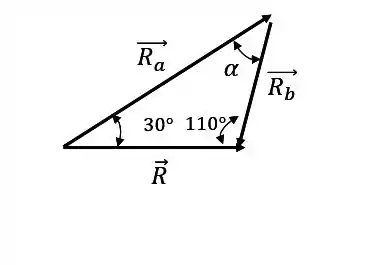
Nós não sabemos o ângulo , mas sabemos que a soma dos ângulos internos de um triângulo é sempre igual a , então:
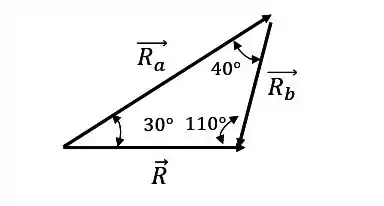
Assim:
Passo 3
Show de bola! Agora vamos aplicar a nossa famosa lei dos senos: Pra cada lado do triângulo, escolha o ângulo que lhe é oposto e monte a equação:
Como sabemos o valor de , basta a gente isolar o que não sabemos:
Passo 4
A projeção de sobre o eixo é mais fácil de se fazer. Basta multiplicar o módulo de pelo cosseno do ângulo que a força faz com o eixo
Assim: