Determine a resultante das duas forças mostradas.
- Aplicando a regra do paralelogramo.
- Somando as componentes escalares.
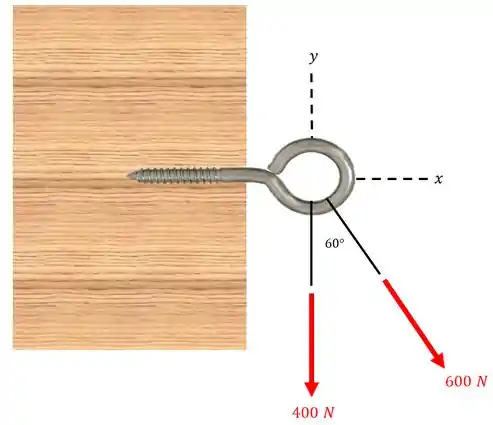
Passo 1
Finalmente vamos usar a nossa querida regra do paralelogramo!!
Nesse caso, é claro, vamos encontrar apenas o módulo da força resultante.
Aplicando a regra:
Passo 2
Agora vamos decompor as forças em suas componentes escalares.
A força de é claramente vertical e aponta no sentido negativo de , assim:
Já a força de precisa ser decomposta segundo o triângulo abaixo:
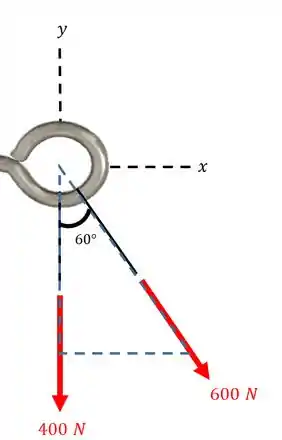
A força faz um ângulo de com o eixo , nesse caso. Mas isso não nos atrapalha, não é mesmo? É Só notar que a componente horizontal será e a vertical . Assim:
Assim, a força resultante será:
E o módulo: