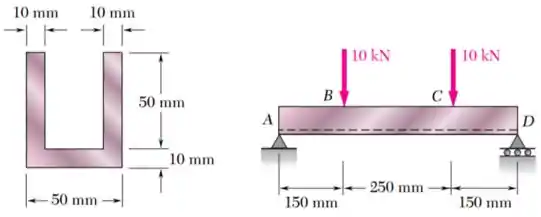
Duas forças verticais são aplicadas à viga com seção transversal mostrada na figura. Determine as tensões de tração e de compressão máximas na parte da viga.
Passo 1
O que está acontecendo?
Existe no trecho da viga um momento fletor (ou só “”) que pode ser encontrado através dos métodos da estática: diagrama de corpo livre, equilíbrio e análise dos esforços internos.
Além disso...
A seção transversal dessa viga tem uma linha neutra de posição e um momento de inércia da área (ou só “”) que podem ser determinados a partir da geometria da seção mostrada.
E o que é que o exercício quer?
Ele quer que a gente determine as tensões de tração e de compressão máximas devido à flexão no trecho da viga.
Essas tensões podem ser encontradas usando a fórmula da flexão:
...onde é a posição do ponto da seção que está sendo avaliado em relação à linha neutra.
Dessa forma, os valores máximos positivo e negativo de (e consequentemente os valores máximos de ) ocorrem para a base e para o topo da seção:
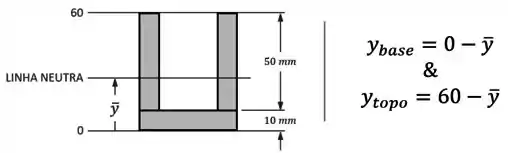
Então para resolver o exercício, devemos:
- Usar os métodos da estática para descobrir o valor de no trecho da viga;
- Encontrar os valores de e para a seção transversal da viga;
- E, finalmente, definir e e calcular as tensões de tração e de compressão máximas usando a fórmula da flexão.
Passo 2
Então vamos começar com o primeiro passo dos métodos da estática, que é o DCL ou:
![]()
Para essa viga:
- O apoio móvel em vai realizar uma reação na vertical ;
- E o apoio fixo em vai realizar uma reação na horizontal (que vai acabar sendo nula e pode ser omitida do DCL) e uma reação na vertical .
Dessa forma, o nosso DCL fica assim:
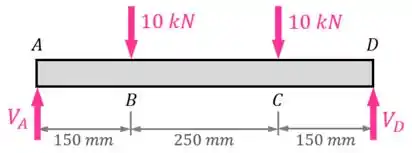
Passo 3
Agora, seguimos para o:
![]()
Aplicando o equilíbrio de forças na vertical, temos:
O que significa que:
Em seguida, aplicando o equilíbrio de momentos em relação ao ponto , temos:
Isolando , encontramos que:
O que significa que:
E, substituindo esse valor na expressão anterior , encontramos que:
Passo 4
Por fim, fazemos a:
![]()
Como nesse exercício, só queremos saber o momento fletor no trecho da viga, só precisamos analisar os esforços internos nas seções desse trecho:
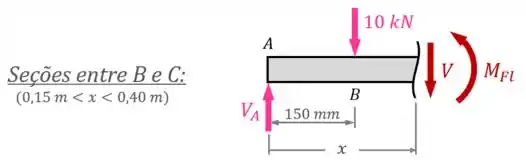
Aí, para encontrar o valor do momento fletor nesse trecho, podemos aplicar o equilíbrio de momentos em relação ao ponto da seção:
Isolando , temos:
Substituindo e fazendo a distributiva, isso fica assim:
Finalmente, cortando com , encontramos que:
Passo 5
Agora, seguimos para a próxima parte do exercício, em que calculamos as propriedades geométricas da seção dessa viga, começando pela:
![]()
Para calcular essa posição, devemos observar a geometria da seção da viga:
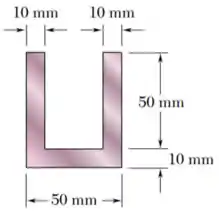
Em seguida, separamos essa geometria em elementos numerados e definimos a base da viga como o ponto :
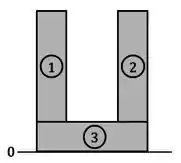
Calculamos as áreas de cada elemento e as posições dos centros de cada um e colocamos esses resultados em uma tabela:
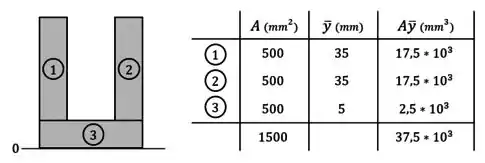
Sendo que, nessa tabela, também colocamos na coluna final os produtos entre esses valores para cada elemento e na linha final os somatórios das áreas e dos produtos .
Com isso, podemos finalmente calcular a posição da linha neutra usando a fórmula:
Substituindo e , encontramos que:
Que é a posição da nossa linha neutra.
Passo 6
Depois da posição da linha neutra, podemos calcular para a seção da nossa viga o:
![]()
Começamos calculando o momento de inércia da área de cada elemento.
Todos os elementos que compõem a seção da nossa viga são retangulares.
Dessa forma, todos eles vão ter momentos de inércia da área .
Para os elementos e , que está “em pé” com uma base e uma altura , vamos ter que:
Já para o elemento , que está “deitado” com uma base e uma altura , temos:
Em seguida, temos que determinar as distâncias entre o centro de cada elemento e a linha neutra:
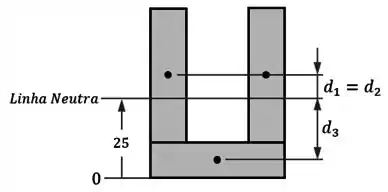
O centro dos elementos e estão a uma altura de , então:
Já o centro do elemento está a uma altura de , então a sua distância vai dar:
Com isso, podemos agora aplicar a fórmula abaixo, baseada no teorema dos eixos paralelos, para determinar o momento de inércia da área da seção transversal como um todo:
Realizando esse somatório, temos:
Substituindo os valores:
- e ;
- e ;
- & ,
E calculando tudo, vamos encontrar que:
Passo 7
Depois de tudo que passamos, chegamos ao passo final, que é definir e e calcular as tensões de tração e de compressão máximas no trecho da viga usando a fórmula da flexão.
Se lembrarmos do que vimos lá no passo 1:
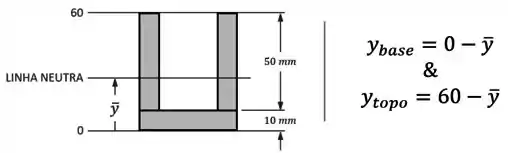
Vamos poder definir agora os valores de e aproveitando o valor da posição da linha neutra que encontramos no passo 5:
Definidos esses valores, sabemos que:
Por um lado, o valor máximo negativo de , vai corresponder à tensão de flexão máxima de tração () no trecho da viga:
Substituindo:
- Do passo , ;
- Do passo , ;
- E do passo atual, ,
- Do passo , ;
- Do passo , ;
- E do passo atual, ,
Vamos encontrar que:
E, como é o mesmo que , isso significa que:
Por outro lado, o valor máximo positivo de , vai corresponder à tensão de flexão máxima de compressão () no trecho da viga:
Daí que, substituindo:
E calculando tudo, encontramos que:
E assim, terminamos o exercício!