A viga representada na imagem está sofrendo um momento .
Determine a posição da linha neutra da seção transversal da viga.
Determine o momento de inércia da área seção transversal da viga.
Calcule as tensões máximas de tração e compressão na viga.
Represente em um gráfico a distribuição de tensão em uma seção transversal da viga.
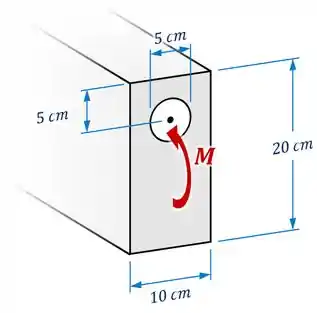
Dica do Expert: O furo circular pode ser considerado como um elemento com uma área negativa e um momento de inércia da área negativo.
Passo 1
O que está acontecendo?
A viga retangular, de base e altura , tem um furo de diâmetro (e, consequentemente, raio .)
É aplicada nela um momento , o que causa nela tensões normais de flexão dadas pela fórmula da flexão:
Onde:
- é a posição do ponto em que se quer avaliar a tensão de flexão em relação à linha neutra da viga;
- & é o momento de inércia da área da seção transversal dessa viga.
E o que é que o exercício quer?
Primeiro, no item , ele quer saber a posição da linha neutra da seção transversal dessa viga, que pode ser encontrada usando a fórmula:
Sendo que uma forma de identificar os termos e dessa equação é numerar o retângulo e o furo da viga e preencher uma tabela como a da figura abaixo:
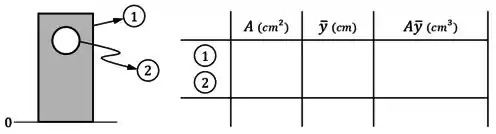
Lembrando que precisamos considerar que o item possui uma área negativa, por se tratar de um furo.
Em seguida, no item , ele quer que a gente calcule o momento de inércia da área para a seção transversal dessa viga.
Para tanto, devemos lembrar:
1. As fórmulas de para elementos retangulares e circulares:
2. Que o valor final de para a viga vai ser dado por:
Onde é o valor de para cada elemento que compõe a viga, a área e a distância do centro de cada elemento (de posição ) à linha neutra (de posição ).
& 3. Que o momento de inércia da área e a área de um furo devem ser contabilizados como negativos.
Depois, no item , o exercício quer que a gente calcule as tensões de flexão máximas de tração () e de compressão () na viga.
Essas tensões máximas ocorrem no topo e na base da seção, que são os pontos com o maior valor positivo e negativo, respectivamente, da posição em relação à linha neutra.
Por último, no item , precisamos desenhar como fica a distribuição de tensões em uma seção transversal dessa viga, o que pode ser feito aproveitando os resultados do item .
Passo 2
Começando pelo item ...
Para determinar a posição da linha neutra, podemos olhar para a figura original do exercício:
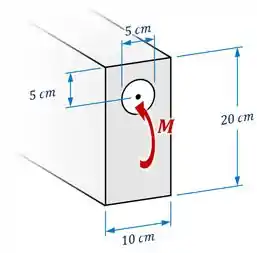
Numerar os elementos que compõem a seção transversal dessa viga e identificar a base da viga como a posição :
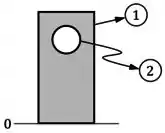
E preencher, em uma tabela, o valor das áreas , das posições dos centros e do produto desses valores de cada elemento, considerando furos como elementos de área negativa:
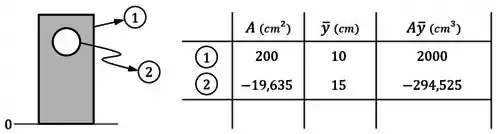
Nessa tabela, a área do círculo foi obtida usando a fórmula e é negativa uma vez que o círculo se trata de um furo.
Por último, fazemos o somatório das áreas e dos produtos e colocamos esses resultados na última linha da tabela:
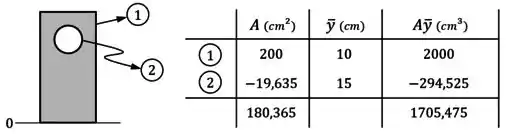
Com isso, podemos finalmente calcular a posição da linha neutra:
E assim, o item está resolvido!
Passo 3
Seguindo com o item ...
Começamos calculando o momento de inércia da área de cada elemento.
Para o elemento , retangular, temos:
Substituindo e , encontramos:
E para o elemento , que é um furo circular, temos:
Substituindo , encontramos:
Em seguida, temos que determinar as distâncias entre o centro de cada elemento e a linha neutra:
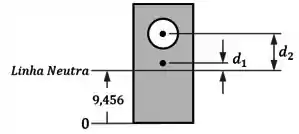
O centro do elemento está a uma altura de , então sua distância vai dar:
E o centro do elemento está a uma altura de , então a sua distância dá:
Com isso, podemos agora aplicar a fórmula abaixo para determinar o momento de inércia da área da seção transversal da viga:
Realizando esse somatório, temos:
Substituindo os valores:
- , e ;
- & , e ,
E calculando tudo, vamos encontrar que:
Que é a nossa resposta para o item .
Passo 4
No item , queremos calcular as tensões de tração () e compressão () máximas nessa viga devido à sua flexão.
Sabemos que essas tensões vão ser regidas pela fórmula da flexão:
E sabemos os valores de (do enunciado) e (do passo anterior).
Ou seja, só falta pensarmos nos valores máximos de para encontrarmos as tensões máximas.
Então vamos pensar...
Por um lado, temos que quando tiver seu valor negativo máximo, vai ter o seu valor positivo (de tração) máximo.
Esse valor negativo máximo de ocorre na base da viga, onde a posição dos pontos em relação à linha neutra vale:
Dessa forma, temos que:
Substituindo:
- ;
- ;
- & ,
Encontramos que:
não é uma unidade usual, então precisamos converter esse resultado para :
Por outro lado, quando tiver seu valor positivo máximo, vai ter o seu valor negativo (de compressão) máximo.
Essa valor positivo máximo de ocorre no topo da viga, onde a posição dos pontos em relação à linha neutra vale:
Dessa forma, temos que:
Substituindo:
- ;
- ;
- & ,
Encontramos que:
Realizando a conversão de para , multiplicamos esse valor por , obtendo:
Passo 5
Resolvido o item , agora só falta desenhar um gráfico para a distribuição de tensões em uma seção transversal da viga para o item .
Considerando um eixo começando na base da nossa viga, sabemos que:
- Na base da viga, onde , ocorre a tensão máxima de tração ;
- Na linha neutra, onde , a tensão é nula; (Isso sempre ocorre na linha neutra!)
- E no topo da viga, onde , ocorre a tensão máxima de compressão .
Marcando esses pontos em um gráfico e sabendo que a tensão varia linearmente com a variação de , ficamos com o gráfico abaixo:
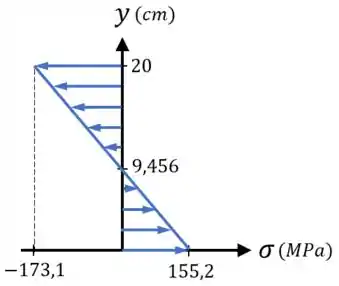
E terminamos o exercício!