Calcule a integral
Passo 1
E aí, preparado para continuar nossos estudos? Então vamos lá!
Deveríamos começar a questão pela integral de dentro , mas ela parece ser muito complicada.
Muitas vezes, quando você não tem a menor ideia de como calcular uma integral dupla, é uma boa tentar mudar a ordem de integração. É o que faremos aqui.
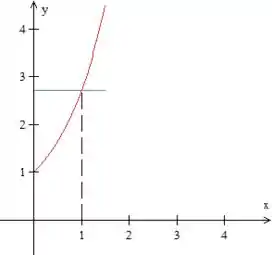
Primeiro, vamos esboçar a região em questão. Perceba que a exponencial corta o eixo em (pois ) e que para . O domínio da integral é essa área entre a curva azul e a vermelha.
Passo 2
Agora vamos reescrever essa região como tipo II, ou seja, vai variar em relação à números e vai estar variando em relação à de funções de . Pelo próprio gráfico, vemos que varia entre e (a reta azul), portanto
Já o valor de varia entre e a reta vermelha, vamos escrevê-la, então, em função de :
Para deixar sozinho, vamos fazer a função dos dois lados, ficando com
Como a função e são funções inversas, elas se anulam, então ficamos com:
Então, temos variando
Nosso domínio será, então:
Passo 3
Podemos, então, reescrever a integral da seguinte forma:
Perceba que a integral ficou muito mais simples agora. 😊
Passo 4
Vamos, agora, integrar em relação a :
Podemos tirar tudo que não é da nossa integral, porque como estamos integrando em relação a vai ser considerado como constante, então temos
Integrando isso temos
Substituindo temos
Que é a mesma coisa que
Podemos cortar os e temos
Show, ficou mais bonitinho
Passo 5
Agora vamos pegar esse resultado e aplicar na integral de fora
Integrando em relação à temos:
Substituindo os valores dos limites de integração, ficamo com
Como podemos escrever o nosso resultado como