Calcule , onde é o triângulo de vértices (-1,0), (0,1) e (1,0).
Passo 1
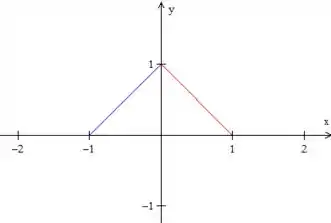
Vamos fazer um esboço desse triângulo para visualizar melhor o problema
Passo 2
Faaala aí, tranquilinho?
Devemos escrever essa região de forma matemática. Perceba varia entre números: e , assim, temos .
Já em , essa área é limitada na esquerda pela reta azul e na direita pela vermelha, certo? Assim, podemos escrever essa região como do tipo II, basta encontrar as equações dessas retas.
Para a reta azul
Temos dois pontos que pertencem a essa reta, e , vamos substituí-los na equação geral de uma reta: . Teremos:
Substituindo o que temos na primeira equação, ficamos com
Substituindo e , vemos que a reta será escrita como . Porém, como nossa região será escrita como do tipo II, devemos isolar o , ou seja, achar em função de .
Para a reta vermelha
Usando o mesmo raciocínio para descobrir a equação dessa reta, vamos substituir os pontos e na equação geral da reta. Teremos:
Substituindo na nossa equação de baixo, ficamos com:
Substituindo e , encontramos . Isolando novamente o , teremos:
Assim, o domínio será escrito como:
E nossos limites, então são
Passo 3
Agora vamos montar a integral! Basta substituir os intervalos que acabamos de encontrar.
Passo 4
Vamos começar então olhando só a integral de dentro!
Integrando isso em relação a (Lembrando que y aqui é como se fosse uma constante) temos:
Vamos substituir então onde tem pelos valores dos limites e subtrair o superior do inferior! Ficamos então com:
Separando os termos da fração, ficamos com
Agora ta mais fácil de juntar os termos em comum né? Então vamo la pra deixar isso mais bonitinho
Passo 5
Shoooow! Vamos pegar o resultado da integral e aplicar na integral de fora!
Essa integral é mais de boinhas de fazer, e fica assim:
Podemos cortar na segunda fração e isso da pra gente
Substituindo os valores dos limites, ficamos com
Então ficamos com
Que é
Pra resolver isso, vamos fazer isso aqui
Que nos dá