Determinar a equação geral do plano que contém as retas
e
Passo 1
O enunciado nos dá as equações de duas retas e e diz que essas duas retas estão no plano que queremos determinar a equação geral. Ent��o, para achar a equação geral do plano devemos determinar dois vetores paralelos ao plano e um ponto pertencente à ele. Os dois vetores paralelos podemos obter por meio do vetor diretor de cada reta.
Vamos começar descobrindo qual é o vetor diretor de cada reta, beleza?!
Passo 2
A reta está escrita na forma de equações reduzidas em função de . Por meio delas conseguimos determinar o jeito genérico dos pontos pertencentes à reta:
Se encontrarmos 2 pontos da reta , conseguimos formar o vetor diretor da mesma, assim:
Assim, o vetor diretor da reta é:
então .
Passo 3
A reta nos é dada em equações paramétricas pois todas as coordenadas e estão em função de . Podemos identificar o vetor diretor facilmente nesse caso, basta observar os coeficientes de :
Assim, .
Passo 4
Dessa forma, analisando as duas retas temos dois vetores:
Opa!!! Mas, esses dois vetores são paralelos, pois . Nesse caso não poderemos usar os dois para determinar o plano!! Como faremos então?
Bom, temos a seguinte figura que representa a situação que temos:
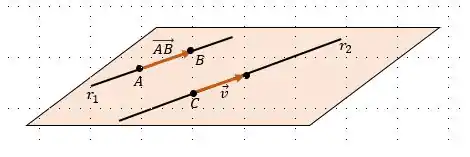
Se e são paralelos, podemos formar um outro vetor que não seja paralelo a eles pegando por exemplo um ponto de e outro de . Por exemplo o vetor !
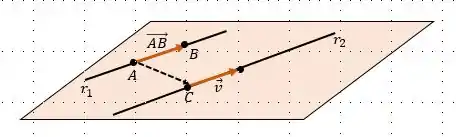
Conseguimos, por meio das suas equações paramétricas, achar um ponto . Com o ponto e , teríamos o vetor:
Assim, escolhendo , entre e já que são proporcionais e o vetor , teremos:
Bom, pelo menos não são proporcionais!!! Ufa!!
Passo 5
Vamos encontrar agora a equação do plano.
Escolhendo como ponto do plano o ponto e os vetores e , agora sim, podemos fazer o produto misto e encontrar a equação geral do plano. Considerando . Teremos .

Pronto!! Chegamos na nossa tão sonhada equação do plano!! hehe
