Determinar a equação geral do plano que passa pelo ponto e é paralelo aos vetores e .
Passo 1
Esse exercício é para esquentarmos bem nossos motores!!haha
O problema nos dá três informações: o ponto que pertence ao plano, e dois vetores paralelos ao plano e . Pela teoria vimos que quando queremos a equação geral e temos um ponto e dois vetores paralelos ao plano basta fazermos o produto misto entre o vetor formado pelo ponto conhecido e um ponto genérico , e os vetores paralelos e igualar a zero.
Passo 2
Então, vamos montar o produto misto entre . Antes, vamos determinar .
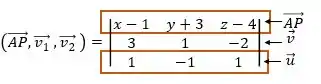
Passo 3
Agora que montamos o produto misto é só resolver:
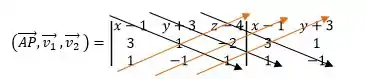
Pronto, chegamos no que queríamos, na equação geral do plano. Podemos também escrever a equação multiplicada por , que ficaria:
As duas estão corretas, o que muda é o sentido do vetor normal, um está apontando para cima e o outro para baixo.