Determine a equação geral do plano que contém os pontos e e é perpendicular ao plano
Passo 1
Queremos determinar a equação geral do plano que contém os pontos e e ainda é perpendicular ao plano , ou seja, forma . Nossa de novo determinar a equação geral do plano??

Isso mesmo!! Porém, a cada questão estamos vendo que o enunciado pode nos dar diferentes dados e que mesmo assim conseguimos obter a equação geral ;).
Nessa questão, por exemplo, vamos nos basear pela figura a seguir.
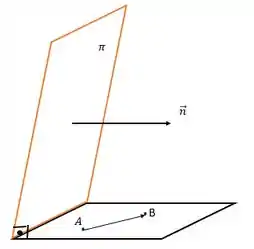
Novamente, para determinar o plano que queremos temos duas opções: ter o vetor normal ao plano e um ponto pertencente a ele OU ter dois vetores paralelos ao plano e um ponto pertencente à ele. Pela figura, podemos ver que vamos ficar com a segunda opção, pois com os pontos e conseguimos formar o vetor que é paralelo ao plano já que eles pertencem ao plano e também podemos notar que o vetor normal do plano é paralelo ao plano que queremos determinar, pois os dois são perpendiculares.
Passo 2
Com tudo o que falamos, acho que deu para sacar que nossos dados serão o vetor , o e um dos pontos ou que poderemos escolher qualquer um deles que o resultado será o mesmo. Vamos determinar então os vetores e :
O vetor tiraremos da equação geral do plano :
Por fim, o ponto que usaremos será o , lembrando que poderia ser o .
Passo 3
Agora, basta montarmos o produto misto entre os vetores e . Sendo um ponto genérico.
Resolvendo:
Prontinho, encontramos a equação geral do plano!!
