O ponto tem coordenadas e a reta passa pelo ponto e é paralela ao vetor . Mostrar que não pertence à reta e determinar a equação do plano que contém e .
Passo 1
O enunciado nos fornece várias informações!! Vamos retirar!!
Dados:
Tendo esses dados devemos mostrar que o ponto não pertence à reta e também devemos determinar a equação do plano que contém e .
Passo 2
Vamos começar mostrando se o ponto pertence ou não á reta . Para isso, como vimos no tópico sobre “Estudo da Reta” devemos montar alguma das equações da reta e testar. Como temos o vetor diretor que é o paralelo a reta e um ponto, vou montar as equações simétricas da reta e testar o ponto .
Substituindo os valores de e , temos:
Passo 3
Agora que já temos as equações simétricas da reta basta substituirmos os valores de e verificar a validade das equações:
Portanto, mostramos que não pertence à
Passo 4
Para finalizar, devemos determinar a equação geral do plano que contém a reta e o ponto
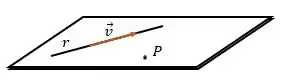
A figura acima mostra o que temos de informações, ou seja, a reta e o ponto que pertence ao plano e sabemos que não pertence à . Mas, vimos que para determinar um plano precisamos do vetor normal e um ponto, ouuu, de dois vetores paralelos ao plano e um ponto. Bem, essa segunda opção me parece a mais viável para o nosso caso!! Um vetor paralelo nós já temos que é o vetor , mas precisamos de mais um!!! Como achar? Se encontrarmos um ponto pertencente à reta e fizermos um vetor com o ponto , teremos:
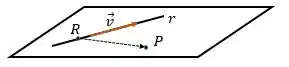
Então, bora achar o ponto pertencente à reta . Para isso vamos usar as equações simétricas que já achamos:
Se chutarmos que , teremos que:
Então, devemos achar e de forma que a proporção seja , assim:
Portanto, temos o ponto .
Passo 5
Agora podemos encontrar o vetor e então teremos as informações necessárias para encontrar a equação geral do plano.
Agora é só montar o produto misto entre o ponto e um ponto genérico e os vetores e .
Montando o produto misto, temos:
Resolvendo,

Vale ressaltar que o ponto da reta escolhido poderia ter sido qualquer outro, que o resultado deve ser o mesmo. Pois, o que importa realmente é que os dois vetores não sejam paralelos entre si e como o ponto não pertence à então não corremos esse risco ;)