Localize graficamente as raízes da equação a seguir:
Passo 1
Mais uma pra localizar as raízes pelo método gráfico. Vamos buscá-las!
Temos a função
Primeiro passo de sempre:
Passo 2
Temo que:
Tá, vamos desenhar o gráfico disso?
O gráfico da é de boa, é uma reta horizontal. Mas e o gráfico de , qual é? Eu pelo menos não sei. Então temos que buscar uma saída, uma forma de achar funções que a gente saiba escrever:
Tem alguma ideia?
Eu tenho:
Passa o dividindo pro outro lado, vai ficar:
Agora sim!
Passo 3
Qual o gráfico de ?
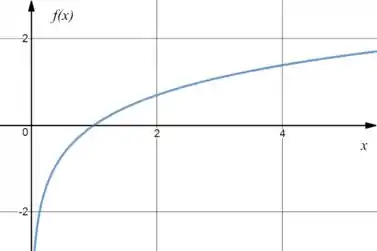
E o gráfico de ?
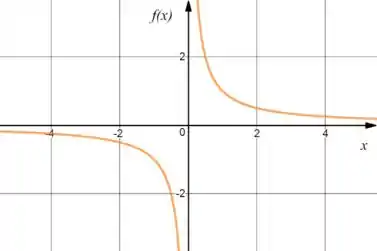
Passo 4
Agora, juntando os gráficos, vamos ter:
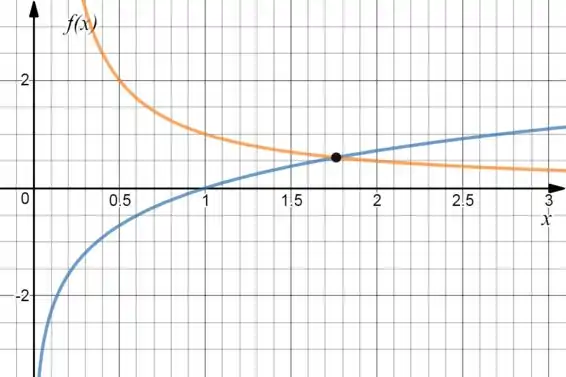
É! Acho que o valor da raiz está ali entre , né?
Como o que nós queremos uma aproximação, acho que uma boa aproximação pra raiz é .