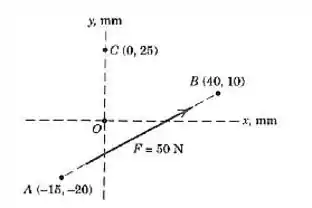
Determine o momento da força de :
- Em relação ao ponto usando o teorema de Varignon.
- Em relação ao ponto por um enfoque vetorial.
Passo 1
Vamos primeiro a escrever a força em termos dos vetores unitários e .
Pra isso, vamos determinar o vetor unitário da linha de ação da força. Esse vetor é o vetor unitário da distância entre
Assim:
Assim, a força é esse vetor multiplicado pelo módulo:
Passo 2
Vamos aplicar o teorema de varignon pra calcular o momento:
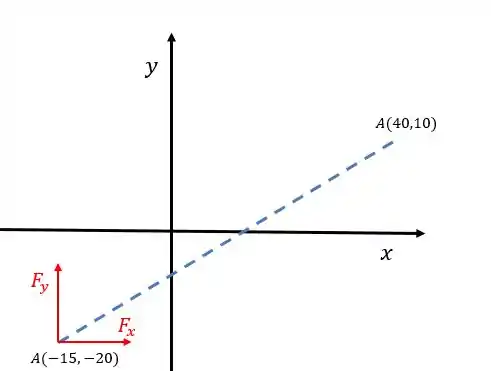
Observe a decomposição da força no ponto. Olhando o sentido de giro de cada componente( gira no sentido anti-horário e no horário) e adotando o sentido anti-horário como o positivo, temos:
Passo 3
b)
Agora queremos saber em relação ao ponto . Vamos usar um enfoque vetorial, ou seja:
E vamos usar a distância entre e como o braço de alavanca:
E :
Porém, nós vamos utilizar Laplace pra calcular o produto vetorial. Assim, é útil escrever os vetores com três dimensões, colocando a componente nula:
Assim:
Os dois primeiros determinantes dão zero, assim: