A força de módulo é aplicada à roda dentada. Determine o momento de em relação ao ponto .
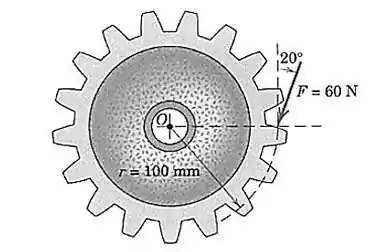
Passo 1
Nosso primeiro passo é decompor a força nos eixos e . Como podemos mover uma força ao longo da sua linha de ação sem alterar o problema, podemos fazer isso aqui para nos facilitar:
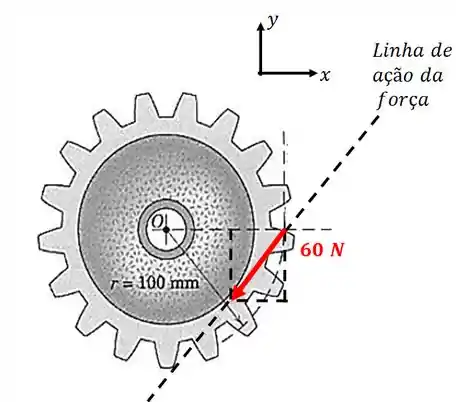
Temos o seguinte triângulo retângulo:
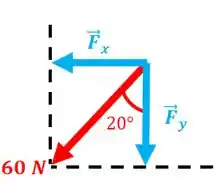
Então:
Passo 2
Agora vamos calcular o momento que cada componente faz em relação ao ponto . Vamos começar pela componente em :
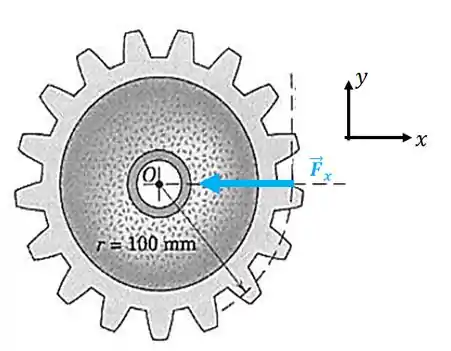
Repare que a distância perpendicular à linha de ação da força até o ponto é zero:
Agora vamos ver a componente em :
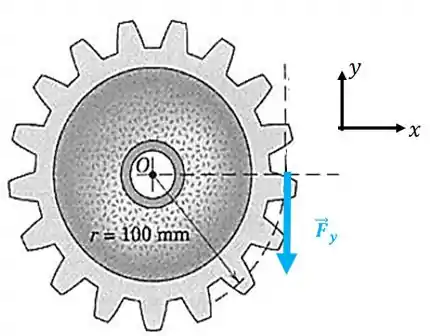
A distância perpendicular entre a linha de ação da força até o ponto é o raio da roda, então:
A força faz a roda girar em torno do ponto no sentido horário, logo esse momento é negativo:
Passo 3
O momento total em relação ao ponto será igual a soma do momento que cada componente faz: