Exercícios de Instalações contendo meios porosos - Lista de Exercícios Resolvida
Questão 1
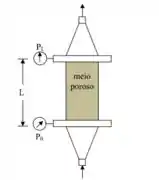
Encontre a expressão para perda de carga no meio poroso:
- Escoamento contra a gravidade
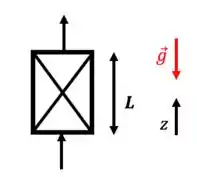
Despreze o termo da equação do movimento!
Ver solução completaQuestão 2
Estimar a capacidade, em , do filtro de areia abaixo esquematizado operando com água a . A primeira camada, com porosidade , é constituída de areia com a seguinte granulometria:
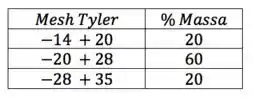
A segunda camada, como porosidade , é constituída de brita com partículas de de diâmetro. As esfericidades da areia e da brita podem ser consideradas como .
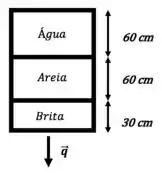
Observação: o filtro é aberto pra atmosfera tanto na entrada como na saída!
Ver solução completaQuestão 3
Simplifique a equação do movimento para achar uma expressão para a queda de pressão no meio poroso em cada um dos casos abaixo:
- Escoamento contra a gravidade
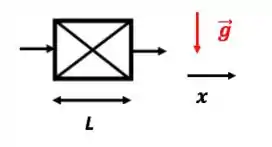
- Escoamento perpendicular à gravidade
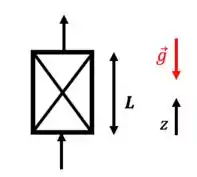
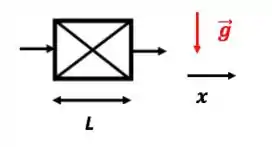
Despreze o termo da equação do movimento!
Ver solução completa