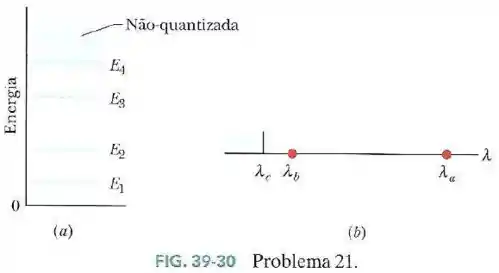
A Fig.39-30a mostra o diagrama de níveis de energia de um poço de potencial unidimensional finito que contém um elétron. A região não quantizada começa em .
A Fig.39-30b mostra o espectro de absorção do elétron quando se encontra no estado fundamental.
O elétron pode absorver fótons com os comprimentos de onda indicados:
, e qualquer comprimento de onda menor que .
Qual é a energia do primeiro estado excitado?
Passo 1
Quando o elétron sai do estado fundamental para os outros estados excitados absorvendo energia, ele absorve um fóton de energia de forma que:
Logo, o comprimento de onda de absorção do elétron está relacionado com a diferença de energia dos estados como:
Quando maior a diferença energética, menor o comprimento de onda. Por isso que para eu tenho e a energia é não quantizada.
Podemos perceber do enunciado também que é o comprimento de onda do fóton absorvido no primeiro estado excitado , é o comprimento para o estado e é o comprimento para o estado . Isso ocorre pois quanto maior o comprimento de onda, menor a energia do estado excitado.
Passo 2
A diferença de energia do estado fundamental para é:
Temos:
Substituindo:
Passo 3
Agora, para achar a energia do primeiro estado excitado, nós usamos o maior comprimento de onda possível. Teremos então:
Onde e pelo passo anterior .
(Apesar da questão não ter pedido, você também poderia ter encontrado a energia do segundo estado excitado , fazendo )