Uma partícula de massa e energia que se move em uma dimensão possui energia potencial que varia com a posição como mostra a figura.
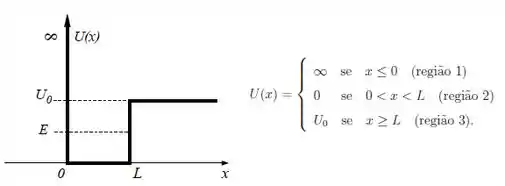
A função de onda estacionária para esta partícula pode ser obtida separadamente em cada região do espaço, sendo assim especificada por:
- Para o caso , escreva a solução geral para , e , expressando-as, quando for o caso, em termos de combinações lineares das funções e , onde as constantes e são ambas reais e positivas.
- Calcule os valores de e como função de , e constantes do problema.
- Que condições de contorno as soluções , e devem satisfazer nos pontos e .
Passo 1
Letra a)
A equação de Schrödinger é sempre:
Para achar as soluções de cada região, nós substituímos a energia potencial e resolvemos essa equação.
Na região , e , a única função de onda possível, para a qual não vamos ter nenhuma inconsistência é .
Na região , e , logo:
Definindo , temos:
Cuja solução é uma combinação de senos e cossenos, o que equivale a uma combinação de exponenciais complexas.
Na região , e , sendo que . Assim, a equação de Schrödinger fica:
Definindo , temos:
Cuja solução é uma combinação de exponenciais reais.
Porém, neste caso, quando , e a função acabaria não sendo normalizável. Por isso, temos que ter .
Passo 2
Letra b)
Pelas definições do item anterior, temos:
Passo 3
Letra c)
As condições de contorno da função de onda são sempre que ela seja contínua. Isso significa que em e tenhamos:
Mas além disso, como e não são zero, também igualamos suas derivadas em , de forma que a derivada da função de onda seja contínua.
Resposta
Letra a)
Letra b)
Letra c)