Um pêndulo simples é afastado da vertical de um ângulo de . O comprimento da corda é de e a massa amarrada à corda é de . Nesta posição inicial o pêndulo sofre um impulso instantâneo que produz uma velocidade inicial tangencial de . Qual é o ângulo onde o pêndulo atinge o repouso instantâneo?

Passo 1
Queremos achar o ângulo final no qual o pêndulo para instantaneamente. Podemos chamar de a distância do pêndulo ao teto nesse instante e de a distância do pêndulo ao teto no começo do movimento.
Vamos fazer um esquema desse pêndulo pra visualizar melhor a questão (e pra você poder apreciar minhas super habilidades no paint, é claro rs):
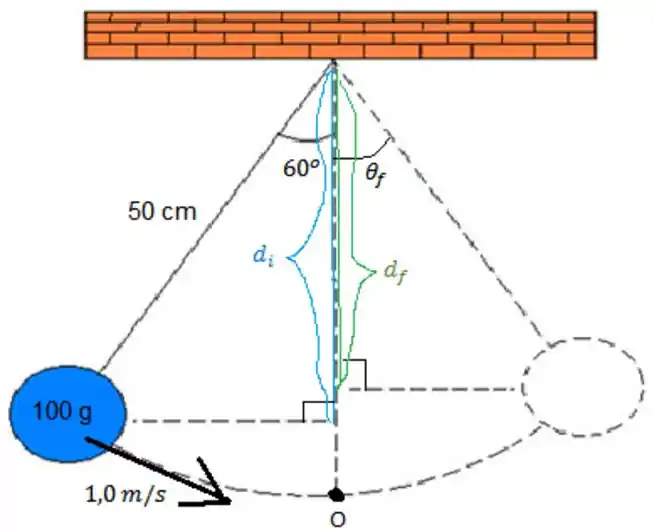
Tá bom, retiro o que disse sobre super habilidades no paint... :)
Passo 2
Vamos calcular essas e ! Com uma trigonometria básica, temos:
Passo 3
Assumindo que não há atrito, podemos tentar aplicar a conservação da energia mecânica:
sendo a energia cinética e a energia potencial. Nesse caso não temos energia potencial elástica, somente energia potencial gravitacional.
Passo 4
Vamos primeiro focar na energia cinética. Temos e .
Então a energia cinética no começo do movimento é:
E no fim do movimento, o pêndulo para por um instante portanto ele não tem energia cinética:
Passo 5
Show, agora vamos dar uma olhada na energia potencial gravitacional.
Vamos definir o zero de potencial na altura do ponto da figura, ou seja abaixo do teto, ok? Então precisamos das alturas e do pêndulo no início e no fim do movimento, respectivamente. Mas como já calculamos e isso vai ser moleza!
é o comprimento do pêndulo menos :
E é o comprimento do pêndulo menos :
Passo 6
Então a energia potencial gravitacional no começo do movimento é:
E quando o pêndulo para:
Passo 7
Excelente! Aplicando a conservação da energia mecânica, vamos ter:
Como e temos , então a equação fica: