Um tubo de aço () com diâmetro externo de e espessura de é colocado em um torno de bancada ajustado de maneira que as mandíbulas apenas toquem as extremidades do tubo sem exercerem nenhuma pressão sobre ele.
As duas forças mostradas na figura são então aplicadas ao tubo.
Após aplicar essas forças, o torno de bancada é ajustado para diminuir a distância entre suas mandíbulas em . Determine as forças aplicadas pelo torno de bancada no tubo em e e a variação do comprimento da parte do tubo.
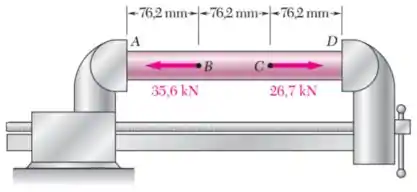
Passo 1
O tubo de aço possui um diâmetro externo e uma espessura . Dessa forma, o tubo possui um diâmetro interno .
A área da seção transversal desse tubo vai ser igual à diferença entre a área do círculo maior, de diâmetro , e a área do círculo menor, de diâmetro .
Como a área de um círculo em função de seu diâmetro é dada por , temos que:
Calculando isso, encontramos que .
Além disso, o tubo ainda tem um módulo de elasticidade e é composto por segmentos que possuem um comprimento inicial .
E o que é que está acontecendo?
Inicialmente, as mandíbulas em e em não fazem nenhuma reação no tubo.
Mas, depois que o tubo é carregado com as cargas e , as mandíbulas fazem forças de reação no tubo para mantê-lo em equilíbrio:
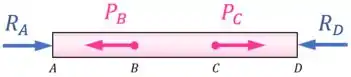
Nessa situação, o tubo é estaticamente indeterminado.
Isso porque só temos uma condição de equilíbrio disponível para usar nele (o equilíbrio de forças na horizontal), mas temos duas incógnitas (as reações e ).
Além de tudo isso, o tubo tem que, após ter sido carregado com todas as forças e reações, ter uma variação de comprimento total .
Isso porque as mandíbulas do torno foram ajustadas de forma a realizar uma compressão de no tubo.
E o que é que o exercício quer?
No item , ele quer que a gente determine as forças aplicadas pelas mandíbulas no tubo, que são as reações e .
Para determinar essas reações, vamos precisar de uma equação de equilíbrio e uma de compatibilidade.
Para encontrar a equação de compatibilidade, vamos usar o método de análise de força para podermos treinar ele.
(Se o seu professor não usa esse método, sinta-se livre para achar a equação de compatibilidade só pensando nas deformações que vão acontecer em cada segmento do tubo!)
Já no item , ele quer saber a variação de comprimento no segmento do tubo, que pode ser encontrada usando a fórmula .
Passo 2
Podemos começar o exercício usando o método de análise de força para determinar a nossa equação de compatibilidade.
Escolhendo a reação como a reação redundante, os diagramas de carregamento e reação redundante ficam assim:
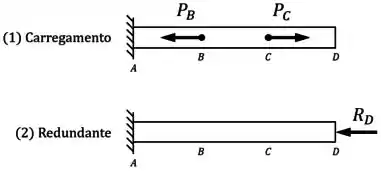
Em seguida, indicamos nesses esboços as variações de comprimento causadas por cada carregamento:
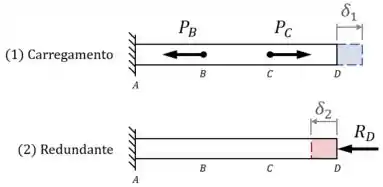
Passo 3
Agora, precisamos definir os valores das variações de comprimento e .
A variação pode ser calculada como a soma das variações em cada segmento:
Usando a fórmula e tendo em mente que os segmentos tem valores iguais para , e , essas variações ficam assim:
Olhando para o diagrama , conseguimos identificar que:
- Como o trecho está sob ação da força de tração e da força de compressão, a sua força interna normal vai ser ;
- Como o trecho só está sob a força de tração, a força interna normal vai ser ;
- E como o trecho não está sob nenhuma força, vamos ter que .
Sendo assim, a variação fica assim:
Arrumando essa expressão, encontramos que:
Já a variação vai ser a variação de comprimento causada em toda a barra pela força :
Aplicando a fórmula para essa variação de comprimento da barra na situação de carregamento do diagrama , ela fica assim:
Normalmente, a força normal na barra nessa situação seria igual à menos a força de compressão:
Mas como no método de análise de força, o sentido das deformações já é indicado nos diagramas, ignoramos esse sinal de negativo e usamos que:
E o comprimento inicial da barra é igual à soma dos comprimentos iniciais dos segmentos , e , que são todos iguais a , de tal forma que:
Sendo assim, a deformação vai ser:
Passo 4
Finalmente, podemos terminar o método de análise de força fazendo a superposição das variações de comprimento nos diagramas e .
Fazendo a superposição da variação para a direita com a variação para a esquerda, encontramos que a variação de comprimento total do tubo vai ser:
Essa é a nossa equação de compatibilidade!
Substituindo as expressões encontradas no passo anterior para e , temos que:
Essa expressão está meio poluída assim, mas se conseguirmos isolar a reação nela, vamos conseguir encontrar o seu valor!
Passo 5
Para isolar na equação anterior, começamos multiplicando os dois lados por :
Isolando , temos que:
Ou seja, vai ser dado por:
Se substituirmos nessa expressão os valores:
- ;
- ;
- ;
- ,
- ;
- E
O resultado para a força vai sair em , já que todos os valores substituídos estão em função das unidades e .
Fazendo essas substituições e calculando tudo, encontramos que:
Passo 6
Agora, para encontrar , podemos recorrer ao diagrama de corpo livre do tubo:
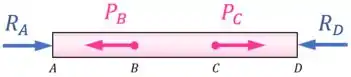
Aplicando o equilíbrio de forças na horizontal, temos que:
Fazendo esse somatório de forças:
Isolando :
Substituindo os valores de , e , temos que:
O que dá:
Os valores que encontramos e são positivos, o que significa que essas reações têm mesmo os sentidos que desenhamos.
E assim finalizamos o item !
Passo 7
No item , o exercício quer saber a variação de comprimento do trecho , .
Usando a fórmula , e tendo em mente que o trecho tem um comprimento inciial , um módulo de elasticidade e uma área de seção transversal , temos que:
Dessa forma, só nos resta descobrir qual é o valor da força interna normal no trecho .
Para tanto, podemos avaliar os esforços internos em uma seção entre os pontos e da peça:
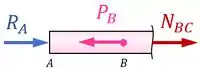
Do equilíbrio de forças na horizontal, temos:
Isolando , encontramos que:
Assim, a deformação vai ser:
Substituindo , , , e , encontramos que: