Seja . Considere as matrizes seguintes:
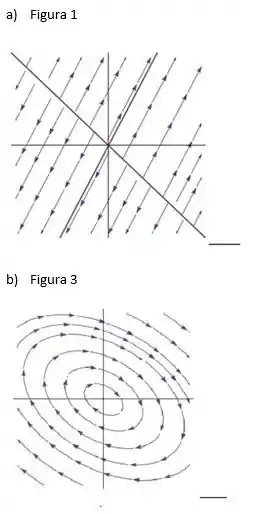
A seguir estão os retratos de fase dos sistemas
Ao lado de cada figura escreva qual é a letra da matriz correspondente.
Passo 1
O macete desse questão é achar os autovalores das matrizes para que assim consigamos descobrir a cara do seu retrato de fase associado.
Vamos fazer cada matriz, uma de cada vez.
- Temos
Então
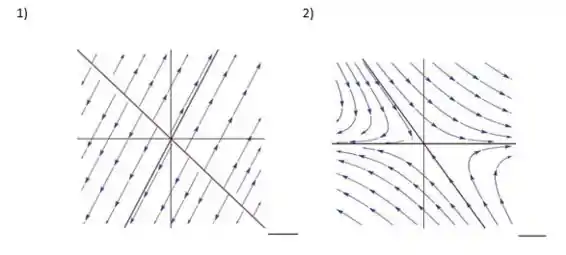
Então como um dos autovalores é zero e o outro é maior que zero, temos um ponto crítico repulsor, então o retrato de fase associado a esse sistema é o da figura (1).
Passo 2
Então,
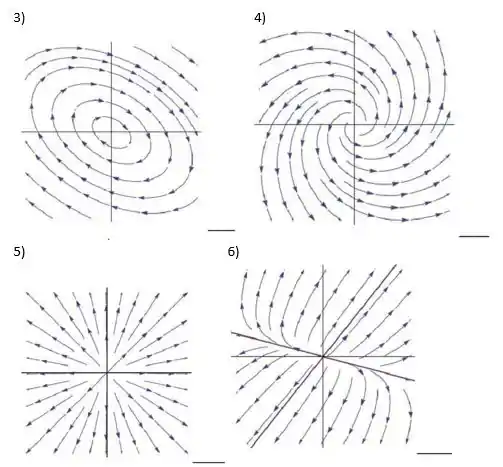
Então, como os autovalores são complexos com parte real nula, temos um ponto crítico do tipo centro, portanto o retrato de fase associado a esse sistema é o da figura (3)
Passo 2
Então,
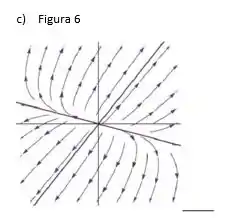
Então, como os autovalores são reais, diferentes e não nulos, temos que o retrato de fase da figura (6) representa o sistema c.
Passo 3
Então,
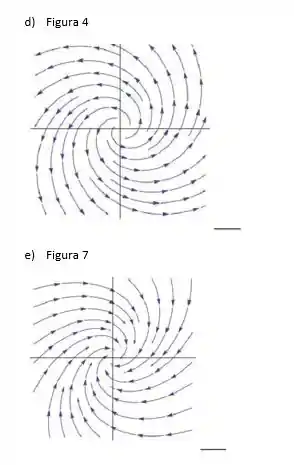
Como os autovalores são complexos com parte real maior que zero, temos uma espiral repulsora e portanto a figura (4) representa o retrato de fase associado ao sistema.
Passo 4
e)
Então,
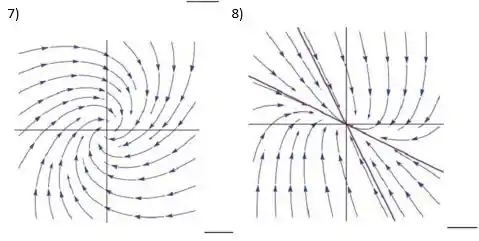
Como os autovalores são complexos com a parte real menor que zero, temos uma espiral atratora portanto a figura (7) representa o retrato de fase associado ao sistema.
Passo 5
f)
Então,
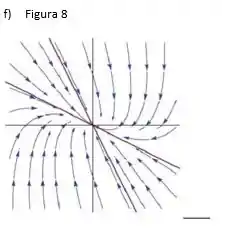
Como os autovalores são negativos e diferentes entre si, temos um nó repulsor ou seja a figura (8) representa o retrato de fase do nosso sistema.
Passo 6
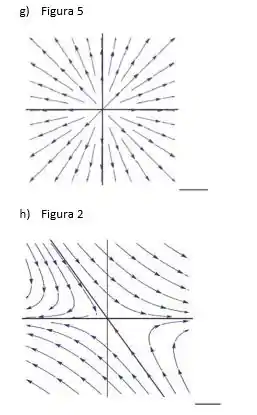
g)
Então, como é uma matriz diagonal, temos que os elementos da sua diagonal são seus autovalores, portanto
Como os autovalores são iguais e diferentes de zero, temos um nó repulsor e portanto a figura (5) representa o retrato de fase do sistema.
Passo 7
h)
Novamente, temos que os autovalores da matriz são os elementos da sua diagonal já é uma matriz triangular superior, portanto
E como temos autovalores reais e com sinais diferentes temos um ponto de sela e portanto a figura (2) representa o retrato de fase do sistema.
Resposta