Sistema de EDO de Dimensão 2 - Retrato de Fase
Para o sistema abaixo, esboce o retrato de fase correspondente e classifique a singularidade
Passo 1
Temos o sistema já no modo matricial, a matriz vai ser
Agora temos que achar os autovalores dessa parada, vamos fazer
Resolvendo essa equação de grau, vamos ter
Temos dois autovalores complexos, onde o sinal da parte real é negativo, o retrato de fase fica algo mais ou menos assim
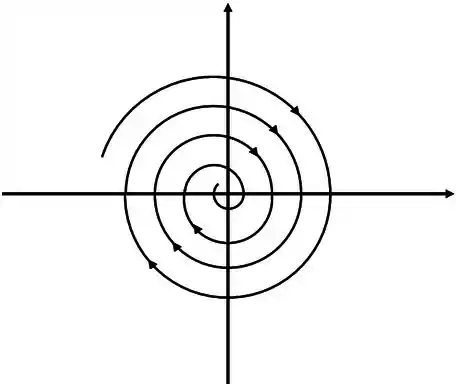
Não precisa calcular os autovetores para fazer esse esboço, como o nome diz é um esboço rs.
O ponto crítico vai ser espiral estável.
Resposta
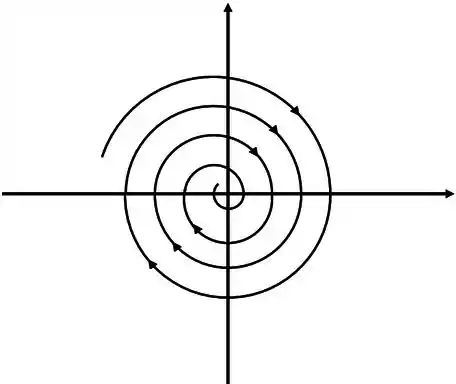
O ponto crítico vai ser espiral estável.
Exercícios de Livros Relacionados
Encontre os pontos críticos.
Em cada um dos problemas de 1 a 4, verifique se (0, 0) é um ponto crítico, mostre que o sistema é localmente linear e discuta o tipo e a estabilidade do ponto crítico (0, 0) examinando o sistema linea
Considere o sistema (2) no texto e suponha que σ1σ2 – α1α2 = 0.Se σ1∊2 – α2∊10, classifique cada ponto crítico e determine se é assintoticamente estável, estável ou instável. Note que o Problema 5 é d
Em cada um dos problemas de 5 a 18:(a) Determine todos os pontos críticos do sistema de equações dado.(b) Encontre o sistema linear correspondente perto de cada ponto crítico.(c) Encontre os autovalor
Em cada um dos problemas de 5 a 18:(a) Determine todos os pontos críticos do sistema de equações dado.(b) Encontre o sistema linear correspondente perto de cada ponto crítico.(c) Encontre os autovalor