Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema da Divergência no Plano

Ver Teoria
Exercício 101234567891112131415

Enunciado

USP, Sem Campus, Cálculo 3, lista 3 - 2022.1, Questão 19d.

19. Calcule o fluxo de   F → através de S ( N → = normal unitária exterior), para:

(d) F → x , y , z = 2 y   i + x - y   j   + 4 x   k , S , onde S é a porção do paraboloide z = x 2 + y 2 - 8 abaixo do plano z = 2 x + 4 y + 3 e N → é a normal exterior ao paraboloide com N → · k → < 0 .

Passo 1

Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉

Nesse problema, temos que calcular o fluxo F → através de uma superfície S que é definida entre o paraboloide z = x 2 + y 2 - 8 abaixo do plano z = 2 x + 4 y + 3 .

Tem ideia de como podemos fazer isso? 🤔

Nesse caso, podemos usar o teorema da divergência.

O teorema da divergência estabelece uma relação entre o fluxo de um campo vetorial através de uma superfície fechada é a divergência desse campo em seu interior.

Matematicamente, o teorema da divergência pode ser enunciado da seguinte forma:

Seja F → um campo vetorial definido em uma região do espaço delimitada por uma superfície fechada S . Então, o fluxo de F → através de S é dado por:

∫ ∫ F → · N →   d S = ∭ d i v F →   d V

A divergência do campo F → é definida por:

d i v F → = ∂ F 1 ∂ x + ∂ F 2 ∂ y + ∂ F 3 ∂ z

Assim, o teorema da divergência estabelece que o fluxo de F → através de S é igual à integral da divergência de F → no interior da região delimitada por S .

Sacou? Bora começar! 😁

Passo 2

Vamos começar calculando o divergente de F →

Se F → x , y , z = 2 y   i + x - y   j   + 4 x   k , então

d i v F → = ∂ F 1 ∂ x + ∂ F 2 ∂ y + ∂ F 3 ∂ z

d i v F → = ∂ 2 y ∂ x + ∂ x - y ∂ y + ∂ 4 x ∂ z

Perceba que as derivadas ∂ 2 y ∂ x e ∂ 4 x ∂ z resultam em 0 , já a derivada de x - y resulta em...

∂ x - y ∂ y = - 1

Substituindo no divergente, temos que

d i v F → = 0 + - 1 + 0

d i v F → = - 1

Substituindo no teorema, temos

∫ ∫ F → · N →   d S = ∭ d i v F →   d V

∫ ∫ F → · N →   d S = ∭ - 1   d V

Portanto, o fluxo de F → através de S nada mais é que o volume V da região multiplicado por - 1 já que ∭ - 1   d V = - 1 · ∭ d V e ∭ d V é o volume de S !

Legal né? 😉

Passo 3

Sabemos que S varia do paraboloide z = x 2 + y 2 - 8 até o plano z = 2 x + 4 y + 3 em que o plano é o limite superior e o paraboloide o limite inferior.

Podemos calcular o volume da região através da integral tripla d V

∫ y i y f ∫ x i x f ∫ z i z f 1 d z d x d y

Vamos esboçar a região S ... esboçando o paraboloide e o plano, temos

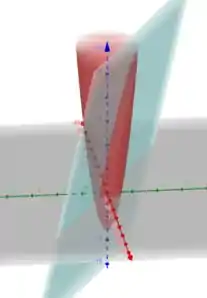
Perceba que olhando de cima, a região é circular, portanto a melhor maneira é aplicar coordenadas polares.

Pra isso, substituímos x por r c o s θ , y por r s e n θ e x 2 + y 2 por r 2 .

Assim, a integral volumétrica é dada como

∫ θ i θ f ∫ r i r f ∫ z i z f 1 d z r d r d θ

A região não é limitada horizontalmente, portanto θ varia de 0 a 2 π .

Igualando as duas equações, vamos obter que r será

x 2 + y 2 - 8 = 2 x + 4 y + 3

x 2 - 2 x + y 2 - 4 y = 3 + 8

x - 1 2 - 1 + y - 2 2 - 4 = 11

x - 1 2 + y - 2 2 = 16

Logo, o paraboloide e o plano se intersectam em um círculo de raio 4 , ou seja, r varia de 0 a 4 .

Substituindo essas informações na integral do volume, temos

∫ 0 2 π ∫ 0 4 ∫ x 2 + y 2 - 8 2 x + 4 y + 3 1 d z r d r d θ

Tranquilo até aqui? 👀

Passo 4

Integrando com relação a z , temos

∫ x 2 + y 2 - 8 2 x + 4 y + 3 1 d z = 2 x + 4 y + 3 - x 2 + y 2 - 8

∫ x 2 + y 2 - 8 2 x + 4 y + 3 1 d z = 2 x + 4 y + 3 - x 2 - y 2 + 8

Substituindo na integral volumétrica

∫ 0 2 π ∫ 0 4 2 x + 4 y - x 2 - y 2 + 11 r d r d θ

Aqui temos que converter nossas coordenadas para coordenadas polares, ou seja

∫ 0 2 π ∫ 0 4 2 r c o s θ + 4 r s e n θ - x 2 + y 2 + 11 r d r d θ

∫ 0 2 π ∫ 0 4 2 r c o s θ + 4 r s e n θ - r 2 + 11 r d r d θ

Aplicando o jacobiano r

∫ 0 2 π ∫ 0 4 2 r 2 c o s θ + 4 r 2 s e n θ - r 3 + 11 r d r d θ

Integrando com relação a r

∫ 2 r 2 c o s θ + 4 r 2 s e n θ - r 3 + 11 r d r = 2 r 3 3 c o s θ + 4 r 3 3 s e n θ - r 4 4 + 11 r 2 2

Aplicando os limites de integração de r ...

∫ 0 4 2 r 2 c o s θ + 4 r 2 s e n θ - r 3 + 11 r d r = 2 4 3 3 c o s θ + 4 4 3 3 s e n θ - 4 4 4 + 11 4 2 2 - 2 0 3 3 c o s θ + 4 0 3 3 s e n θ - 0 4 4 + 11 0 2 2

∫ 0 4 2 r 2 c o s θ + 4 r 2 s e n θ - r 3 + 11 r d r = 128 3 c o s θ + 256 3 s e n θ - 64 + 88

Está acompanhando? 🤔

Passo 5

Substituindo o resultado da integral volumétrica.

∫ 0 2 π 128 3 c o s θ + 256 3 s e n θ + 24 d θ

Por fim, integrando com relação a θ

∫ 128 3 c o s θ + 256 3 s e n θ + 24 d θ = 128 3 s e n θ - 256 3 c o s θ + 24 θ

Aplicando os limites de integração

∫ 0 2 π 128 3 c o s θ + 256 3 s e n θ + 24 d θ = 128 3 s e n 2 π - 256 3 c o s 2 π + 24 2 π - 128 3 s e n 0 - 256 3 c o s 0 + 24 0

∫ 0 2 π 128 3 c o s θ + 256 3 s e n θ + 24 d θ = 0 - 256 3 + 48 π - 0 - 256 3 + 0

∫ 0 2 π 128 3 c o s θ + 256 3 s e n θ + 24 d θ = 48 π

Portanto, voltando ao teorema da divergência, temos que

∫ ∫ F → · N →   d S = ∭ - 1   d V

∫ ∫ F → · N →   d S = - 48 π

É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍

Resposta

∫ ∫ F → · N →   d S = - 48 π

Exercícios de Livros Relacionados

Os pontos P 1 e P 2 são fontes ou sorvedouros no campo vetorial F → mostrado na figura? Dê uma explicação baseada exclusivamente na figura.Dado que F → x , y = x , y 2 , use a definição de divergente
Supondo que v → representa a velocidade de um fluido em movimento, verificar se v → representa um possível fluido incompressível.a) v → x , y = 2 y - 3 i → + x 2 j →
Use o Teorema do Divergente para calcular ∬ S2 x + 2 y + z 2 d S onde S é a esfera x 2 + y 2 + z 2 = 1 .
Demonstre cada identidade, supondo que S e E satisfaçam as condições do Teorema do Divergente e que as funções escalares e as componentes dos campos vetoriais tenham derivadas parciais de segunda orde
Demonstre cada identidade, supondo que S e E satisfaçam as condições do Teorema do Divergente e que as funções escalares e as componentes dos campos vetoriais tenham derivadas parciais de segunda orde