USP, Sem Campus, Cálculo 3, lista 3 - 2022.1, Questão 21e.
21. Calcule as seguintes integrais:
(e) , onde é a parte de com , orientada com a normal unitária tal que
Passo 1
Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎
Nesse problema, queremos obter a integral da função vetorial
através de uma superfície dada por limitada entre .
Tem ideia do que podemos fazer? 🤔
Ao invés de calcularmos o vetor normal a podemos aplicar o teorema da divergência pra resolver esse problema.
O teorema da divergência estabelece uma relação entre o fluxo de um campo vetorial através de uma superfície fechada é a divergência desse campo em seu interior.
Matematicamente, o teorema da divergência pode ser enunciado da seguinte forma:
Seja um campo vetorial definido em uma região do espaço delimitada por uma superfície fechada . Então, o fluxo de através de é dado por:
A divergência do campo é definida por:
Assim, o teorema da divergência estabelece que o fluxo de através de é igual à integral da divergência de no interior da região delimitada por .
Sacou? Bora começar! 😁
Passo 2
Como não é uma superfície fechada, temos que adicionar algumas integrais de linha para fechar .
é dada por um cone circular
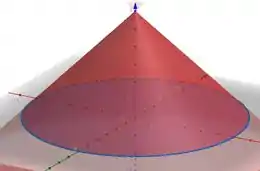
Então para fechar a região, temos que aplicar uma outra superfície na base de , em , ou seja
Uma circunferência de raio .
Atualizando o teorema, adicionando a integral de linha de
Agora vamos calcular o divergente de
Pela regra do quociente as derivadas são
Logo
Entendeu essa parte? 😉
Passo 3
Dessa forma, a integral de linha de é dada por
Como é uma superfície paralela ao plano e o vetor normal aponta para fora da superfície será dado por
Aplicando na integral de
Como estamos em em então
Assim, substituindo no teorema, temos que e, portanto...
Fim! Iae, o que achou? Responde Aí! 😁
