Resolva o seguinte problema de valor inicial por Transformada de Laplace. Indique sempre a propriedade da tabela de transformadas de Lalace sendo utilizada em cada passo.
Passo 1
Fala povo, tudo certinho? Vamos lá? Pra começar, quando usamos transformadas, podemos fazer a transformada nos dois lados da equação:
E das propriedades das transformadas, podemos ainda fazer:
Opa, transformadas! Vamos ver uma de cada vez, ok? Na ordem de leitura, usamos a propriedade pra fazer a primeira transformada:
![]()
Sendo assim, temos:
Do enunciado, tiramos os valores da função para e da sua derivada no mesmo instante:
Show, agora pra segunda transformada a ideia vai ser a mesma, usaremos também a regra :
Pras outras duas, vamos usar as propriedades e , respectivamente:

Sendo assim, vamos ficar com:
Juntando tudo, temos:
E rearrumando isso, temos:
E nos próximos passos a gente vai se preocupar em inverter pra achar ! Vamo que vamo!
Passo 2
Pra começar, a mesma propriedade que vimos pra transformada, vale pra transformada inversa! Ou seja galera, vamos ficar com essa fórmula linda aqui:
Temos então três transformadas inversas pra achar! Pra primeira, podemos usar a propriedade da integral de convolução:
![]()
Onde:
E o produto desses dois será o interior da nossa primeira transformada inversa:
Sendo assim, como:
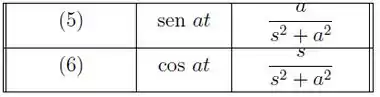
Temos:
A integral de convolução fica:
Das propriedades trigonométricas, tiramos que:
EITA, enrolou agora! Calma galera, nada que fazer uma integral de cada vez não resolva. Pra primeira, temos:
Pra segunda, temos:
A integral fica:
Juntando essa bagunça toda, temos:
Passo 3
Ok eu sei, o passo anterior foi beeeeem doido, mas calma que sobraram só transformadas mais tranquilas pra gente. Saca só:
A primeira sai se usarmos as propriedades

Sendo assim, temos:
Juntando os dois resultados acima, temos:
E por último, temos:
Que sai direto usando a propriedade . Misturado tudo da pra ver, um resultado aparecer: