Calcule as reações dos apoios em e para a viga submetida às duas cargas distribuídas com variação linear.
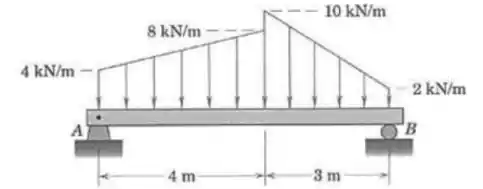
Passo 1
Primeiro vamos montar o diagrama de corpo livre:
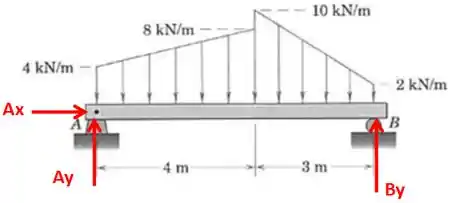
Agora temos que transformar essas forças distribuídas em forças pontuais. Repare que temos dois trapézios. Então, vamos dividir cada trapézio em um retângulo e um triângulo, assim:
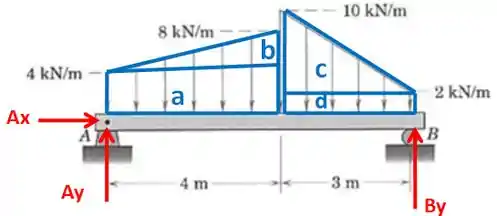
Vamos chamar cada área de , , e e vamos calcular suas resultantes:
- Área
- Área :
- Área :
- Área :
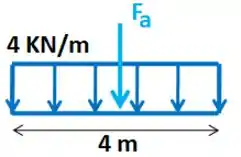
Sabemos que a força resultante fica na metade do comprimento do retângulo:
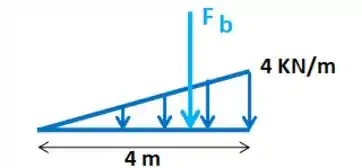
Essa força resultante fica localizada à da altura do triângulo, então:
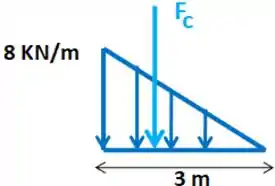
Quando temos um triângulo, a força resultante fica à da altura:
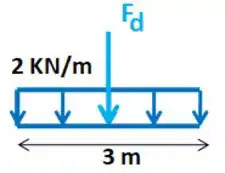
A posição da força resultante é:
Então, como ficou nosso diagrama de corpo livre no final das contas?
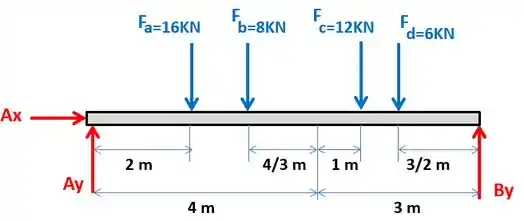
Passo 2
Precisamos agora escolher um ponto de referência para calcular os momentos. Vamos escolher o ponto :
Passo 3
Nosso próximo passo é fazer o somatório das forças. Repare que a única força horizontal é a nossa reação , logo ela será nula. Escrevendo matematicamente, temos:
Agora vamos fazer o somatório das forças na vertical: