Calcule a área da superfície obtida pela revolução da curva em torno do eixo .
Passo 1
Rotação de uma curva em relação ao eixo , né? O enunciado nos pede a área da superfície gerada, isso é exatamente o tipo de questão pra usarmos o teorema de pappus! Como já temos a nossa superfície parametrizada, vamos aplicar direto o teorema!
É válido a gente fazer o esboço do gráfico para saber se a área é igual a rotação completa da curva, lembra? No nosso exercício a curva é assim:
E a superfície gerada é essa aqui:
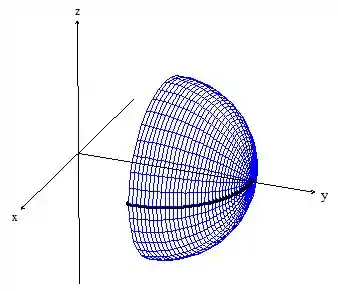
Percebe que precisamos dar a volta completa dessa curva para gerar a superfície, certo? Portanto usamos a fórmula do teorema de pappus normalmente:
Usamos módulo de porque a rotação é ao redor do eixo , lembra?
Beleza, então precisamos tirar esse módulo de dentro da integral, calcular o valor de e depois resolver a integral, vamos lá?
Passo 2
Vamos tirar o módulo da integral, primeiro, para isso precisamos analisar se é positivo ou negativo no intervalo dado!
A função é sempre positiva nesse intervalo, certo? Então, para todo o intervalo:
Passo 3
Precisamos calcular o valor de , para isso, vamos derivar a parametrização da curva:
Passo 4
Voltando para a nossa integral: