Exercícios de Área de Superfícies - Lista de Exercícios Resolvida

Calcule a área da superfície obtida pela revolução da curva em torno do eixo .

Calcule a área da superfície obtida pela revolução da curva em torno do eixo no intervalo

Seja o segmento da reta com no plano .

Considere a superfície de revolução obtida girando em torno do eixo .

Determine a sua área.

Encontre a área da calota cortada do hemisfério , pelo cilindro .

Determine a área da superfície , , .O

Compute o fluxo do campo vetorial aravés da esfera unitária .

Considerando a superfície dada pela porção do cone limitada pelos planos e .c) Determine a área da superfície .

Seja a superfície parametrizada

(a) Calcule a equação implícita para a imagem de .

(b) Esboce a imagem de .

(c) Justifique se a imagem de é uma superfície regular ou não. Calcule o plano tangente à imagem de no ponto

(d) Calcule a área de

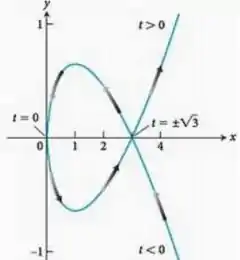
Questão 2) Calcule a área delimitada pela curva

Conforme a figura a seguir:

Calcule a área da superfície de revolução gerada pela curva plana definida pela equação

em torno da reta paralela ao eixo passando pelo ponto .

Calcule a área da superfície obtida pela revolução em torno do eixo- da curva parametrizada por

Questão 1) Seja a curva dada por

Determine a érea da região delimitada por .

Questão 4) Sejam e positivos. Determinar a área delimitada pela curva simples e fechada

Calcule a integral onde é a fronteira (orientada positivamente) da região delimitada pelas curvas e no primeiro quadrante.

Questão 3) Calcule:

b) A área delimitada pela curva dada ela parametrização onde

Calcule , onde e é a interseção do plano com o cilindro . (Oriente C no sentido anti-horário quando visto de cima).

Encontre a área da superfície obtida girando-se uma curva plana em torno do eixo