1. Dado o sistema linear:
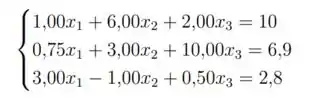
- Reescreva o sistema linear de forma a garantir sua convergência pelo método de Jacobi (diagonal estritamente dominante por linha).
- Escreva as expressões das sequências obtidas pelos métodos de Jacobi e Gauss-Seidel (i.e., o motor gerador de cada incógnita) para o problema acima.
- Calcule duas iterações do método de Gauss-Seidel com vetor inicial x(0) = (0; 0; 0)T .
Passo 1
Oiii, pessoal! De boa? Mais uma provinha de cálculo numérico! Nesse primeiro exercício, lembraremos de alguns métodos iterativos para aproximar a solução de um sistema linear, o método de Jacobi e o método de Gauss Seidel!
Esses dois métodos partem de um vetor inicial, mas nem sempre eles irão convergir para uma solução, por mais que a gente faça um zilhãoooo de iterações! Uma das formas de garantir essa convergência é obtendo um sistema cuja matriz de coeficientes possui a diagonal estritamente dominante por linha.
Mas pera lá, o que é isso? Basicamente, o módulo do elemento de cada linha que fica na diagonal principal tem quer ser maior do que a soma dos módulos dos demais elementos da linha. Note que, na segunda linha do nosso sistema, e o elemento da diagonal principal e o . Pra que essa linha satisfaça a condição de convergência, precisamos que . Mas , ou seja, essa linha não satisfaz a condição de convergência!
Uma forma de ajustar esse sistema para que ele satisfaça a condição de convergência, é mudar a ordem das linhas. Dá uma olhada:
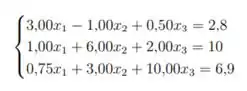
Neste caso, , e ! Ou seja, os elementos da diagonal são maiores que a soma dos outros elementos de suas linhas. Logo, o sistema acima converge pele método de Jacobi, o que responde a letra A!
Passo 2
Já podemos então seguir para o enunciado da letra B! Para obter as expressões das sequências no método de Jacobi, devemos isolar a incógnita na linha 1, na linha 2 e na linha 3:
O indica qual é o vetor solução que a incógnita pertence, em termos de iteração. Por exemplo, para , a solução aproximada depende dos valores do vetor inicial . Isto é, o cálculo do novo vetor solução depende do vetor solução anterior! De boa, né, galera?
No método de Gauss Seidel, esta relação é um pouquinhoooo diferente. Agora, o cálculo do novo vetor solução vai depender de seus próprios valores! QUE? Como assim?
Bem galera, não é difícil! Concorda que para calcular , nós precisamos de e do vetor solução anterior? Beleza, eu também concordo! Mas para calcular nós podemos usar o valor de que acabamos de calcular (mas o tem que usar o da iteração anterior mesmo)! Da mesma forma, na hora de calcular , já vamos ter calculados e , então podemos usar esses valores mais atualizados da iteração atual. Com isso, nossas iterações são otimizadas :) Vamos obter algo assim:
Passo 3
Beleza, pessoal, a questão C pede duas iterações do método de Gauss Seidel. Ou seja, queremos obter os vetores e . Vamos nessa!
Lembrando que o valor inicial e x(0) = (0; 0; 0)T
Iteração 1:
=
=
Iteração 2:
=
=
E é isso, pessoal! Moleza ;) Até a próxima!
Resposta
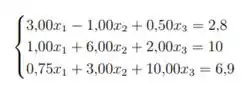
- Jacobi:
- e .
Gauss-Seidel: