Exercícios de Cone e Parabolóides - Lista de Exercícios Resolvida

Esboce o gráfico da quádrica a seguir:

Identifique as superfícies quadráticas abaixo e esboce seu gráfico.

Identifique essa Quádrica e faça seu esboço

Faça um esboço da superfície, destacando as curvas de interseção com os planos coordenados , e .

Considere a quádrica a seguir:

Identifique a quádrica, encontre os traços, determine as seções e esboce seu gráfico.

Ache a superfície de ponto tais que a distância de ao ponto é a mesma do que a de ao plano .Identifique a superfície.

Ache a superfície de ponto , cuja distância ao eixo é 2/3 da distância de ao plano . Identifique a superfície.

Associe cada quádrica ao gráfico que mais se assemelha a ela:

e

Faça um esboço das superfícies e , separadamente, destacando as curvas de interseção com os planos coordenados , e .

Considere a superfície dada pela equação

Para qual valor de abaixo a superfície é um paraboloide elíptico?

5. Nenhuma das demais alternativas.

Considere as duas superfícies dadas por e .

1. Esboce, separadamente, as duas superfícies, mostrando as curvas de interseção com os planos coordenados.

Seja a superfície de equação . Considere as afirmativas:

1. É um paraboloide hiperbólico e sua equação padrão é .
2. É um hiperboloide de uma folha e sua equação padrão é .
3. Seu gráfico é:

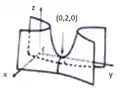
Assinale a opção correta, onde V é verdadeiro e F é falso:

1. Nenhuma das demais respostas
2. (I)F, (II)F, (III)F
3. (I)V, (II)F, (III)V
4. (I)F, (II)V, (III)F
5. (I)F, (II)F, (III)V

A superfície de equação é:

1. Um hiperboloide de duas folhas
2. Um hiperboloide de uma folha
3. Um cone elíptico
4. Um paraboloide hiperbólico
5. Um paraboloide elíptico

A equação descreve um:

paraboloide elíptico;

cone

elipsoide

paraboloide hiperbólico

hiperboloide

O conjunto dos pontos equidistantes do ponto e do plano é composto por

1. Um elipsoide
2. Um plano
3. Dois planos
4. Um hiperboloide
5. Um paraboloide

Determine uma equação da superfície obtida pela rotação da “parábola” em torno do eixo .

Seja o conjunto de pontos em tal que a distância de ao ponto é a mesma que a distância de ao plano . Então é:

1. Não existe superfície
2. O cone
3. O hiperboloide
4. A esfera
5. O paraboloide

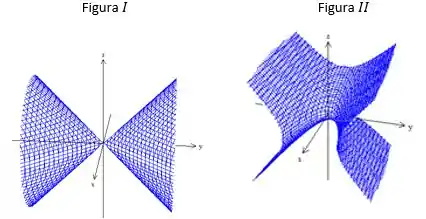
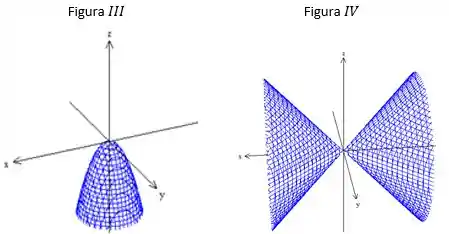
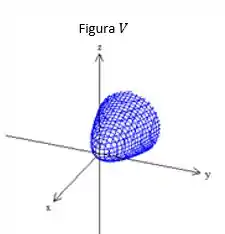
Dentre as figuras abaixo aquelas que associam corretamente e superfície são:

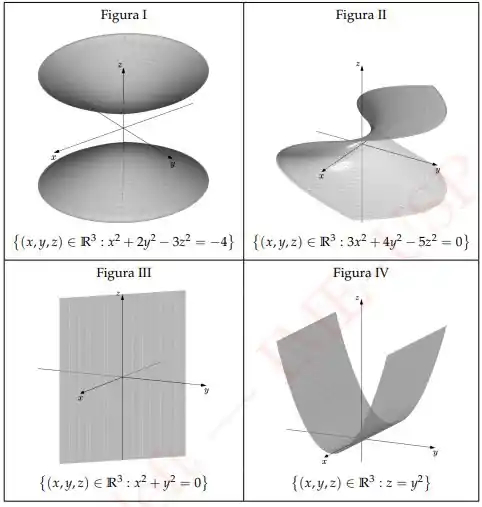
a) I e IV.

b) I e II.

c) I e III.

d) II e IV.

e) III e IV.

Dentre as figuras abaixo aquelas que associam corretamente e superfície são:

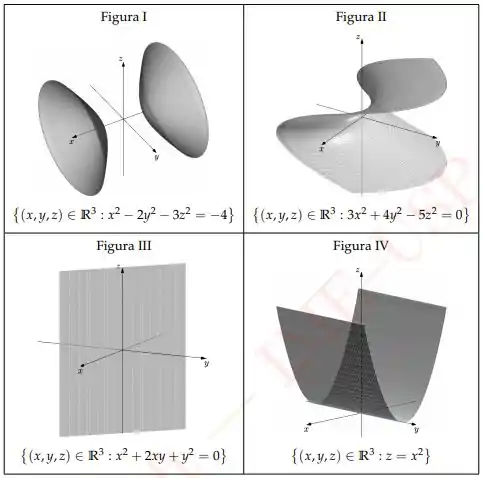
a) III e IV.

b) I e II.

c) I e III.

d) II e IV.

e) I e IV.

Sejam as superfícies dadas pelas equações implícitas

e seja a região limitada pelas superfícies e que contém a origem.

a) Faça o esboço da regição

b) Calculea seguinte integral tripla:

Dentre as figuras abaixo aquelas que associam corretamente e superfície são:

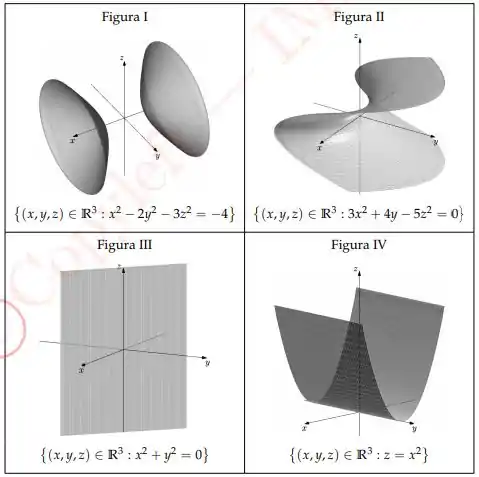
a) II e IV.

b) I e II.

c) I e III.

d) III e IV.

e) I e IV.

Considere a superfície definida por:

1. Faça um desenho da superfície, destacando as curvas de interseção com os planos

Considere as superfícies:

1. Esboce o gráfico de e separadamente, contendo no mínimo curvas com destaque.

Esboce o gráfico de

Restrito à região a partir da interseção com os planos e

Qual das superfícies abaixo de (I) a (V) corresponde ao gráfico da quádrica ?

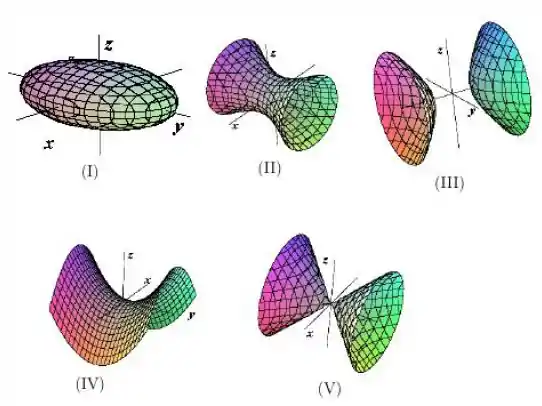
a) III

b) II

c) I

d) IV

e) V