Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Integração

Ver Todos os Exercícios

Teoria

Como Calcular?

Ai gzuiss, dá pra integrar vetor também?

Claro que dá!

Mas como???

Muito fácil. Quando queríamos derivar um vetor não era só derivar cada componente? Então, pra integrar é a mesma coisa, assim:

σ t = x t ,   y t ,   z t

∫ a b σ t d t = ∫ a b x t d t ,   ∫ a b y t d t ,   ∫ a b z t d t

Por exemplo:

σ t = t + 1 , t 2 , e t

∫ 1 2 σ t d t = ∫ 1 2 t + 1   d t ,   ∫ 1 2 t ² d t ,   ∫ 1 2 e t d t

∫ 1 2 σ t d t = t 2 2 + t 2 1 , t 3 3 2 1 ,   e t 2 1

∫ 1 2 σ t d t = 2 2 2 + 2 - 1 2 2 + 1 , 2 3 3 - 1 3 3 ,   e 2 - e 1

∫ 1 2 σ t d t = 5 2 , 7 3 ,   e 2 - e 1

Mas fica ligado, porque as vezes a gente pode ter uma integral indefinida.

∫ σ ( t ) = ∫ x t d t ,   ∫ y t d t ,   ∫ z t d t

Nesse caso, teremos que adicionar uma constante na integração de cada componente, de modo que o vetor final será

∫ σ t = R t + C

Onde

R t = ∫ x t d t ,   ∫ y t d t ,   ∫ z t d t

C = ( c 1 , c 2 , c 3 )

Sendo c 1 , c 2 , c 3 as constantes resultantes da integração indefinida de cada uma das componentes.

Vou te dar um exemplo pra clarear as ideias:

σ t = t + 1 , t 2 , e t

∫ σ t d t = ∫ t + 1 d t ,   ∫ t 2 d t ,   ∫ e t d t

∫ σ t d t = t 2 2 + t + c 1 , t 3 3 + c 2 ,   e t + c 3 = t 2 2 + t , t 3 3 , e t + c 1 , c 2 , c 3

∫ σ t d t = t 2 2 + t , t 3 3 , e t + C

Sacou?

Se liga no que vou te falar agora então:

Lembra que o vetor velocidade é a derivada do vetor posição de uma partícula e o vetor aceleração é a derivada do vetor velocidade?

v → t =   σ ' ( t ) = x ' ( t ) ,   y ' ( t ) ,   z ' ( t )

a → t =   v → ' ( t ) = x ' ' ( t ) ,   y ' ' ( t ) ,   z ' ' ( t )

Então, agora que a gente já sabe integrar vetores, podemos recuperar a velocidade de uma partícula a partir de sua aceleração e a posição, a partir de sua velocidade.

v → t = ∫ a → ( t )

σ t = ∫ v → ( t )

Vê se você entendeu:

Se a aceleração de uma partícula é dada por

a → t = ( - 3 cos ⁡ t ,   - 3 s e n   t ,   2 )

E sabemos que, no instante t = 0 ela saiu do ponto ( 3,0 , 0 ) com velocidade v → 0 = ( 0,3 , 0 ) , qual o vetor posição dessa partícula?

Integrando a aceleração, encontramos a velocidade:

∫ a → t = v → t = - 3 s e n   t ,   3 cos ⁡ t , 2 t + ( c 1 , c 2 , c 3 )

Pra descobrir essas constantes ai a gente usa o fato de que v → 0 = ( 0,3 , 0 ) :

- 3 s e n 0 + c 1 = 0

3 cos ⁡ 0 + c 2 = 3

2 ( 0 ) + c 3 = 0

Então:

c 1 = 0

c 2 = 0

c 3 = 0

Assim, a velocidade da partícula é

v → t = - 3 s e n   t ,   3 cos ⁡ t , 2 t

Agora, integrando a velocidade, encontramos o vetor posição:

∫ v → t = σ t = 3 c o s   t ,   3 sen ⁡ t , t 2 + ( c 1 ,   c 2 , c 3 )

Pra descobrir essas constantes ai a gente usa o fato de que σ 0 = ( 3,0 , 0 ) :

3 cos ⁡ 0 + c 1 = 3

3 s e n   0 + c 2 = 0

t 2 + c 3 = 0

Então:

c 1 = 0

c 2 = 0

c 3 = 0

Assim, o vetor posição da partícula é

σ t = 3 c o s   t ,   3 sen ⁡ t , t 2

Tranquilo? Vamos para os exercícios então.

Exercícios Resolvidos

Exercício Resolvido #1

Hamilton Luiz Guidorizzi, Um curso de cálculo, Volume II, 5ª ed. Rio de Janeiro: LTC, 2001, pg.136, exercício 12b.

Determine r ( t ) sabendo que

r ' t = s e n   t , c o s   2 t   , 1 t + 1 ,   t ≥ 0

r 0 = ( 1 , - 1,2 )

Passo 1

A gente já sabe que pode recuperar r ( t ) a partir de sua derivada r ' ( t ) , assim:

r t = ∫ r ' t d t = ∫ s e n   t   d t ,   ∫ c o s 2 t   d t , ∫ 1 t + 1 d t

r t = - c o s   t   , s e n 2 t 2 , l n   t + 1   + ( c 1 , c 2 , c 3 )

Passo 2

Agora, para descobrir essas constantes ai a gente usa o fato de que r 0 = ( 1 , - 1,2 ) :

- c o s   0   + c 1 = 1

s e n 2 ( 0 ) 2 + c 2 = - 1

l n   0 + 1   + c 3 = 2

Resolvendo cada uma dessas equações, chegamos a:

c 1 = 2

c 2 =   - 1

c 3 = 2

Passo 3

Assim,

r t = - c o s   t   , s e n 2 t 2 , l n   t + 1   + ( c 1 , c 2 , c 3 )

r t = - c o s   t   , s e n 2 t 2 , l n   t + 1   + ( 2 , - 1,2 )

r t = 2 - c o s   t   , s e n 2 t 2 - 1 , l n   t + 1 + 2  

Resposta

r t = 2 - c o s   t   , s e n 2 t 2 - 1 , l n   t + 1 + 2  

Exercício Resolvido #2

Hamilton Luiz Guidorizzi, Um curso de cálculo, Volume II, 5ª ed. Rio de Janeiro: LTC, 2001, pg.139, exercício 2, itens a,b.

Sejam

F t = t , 1 , e t

G t = ( 1,1 , 1 )

Calcule

  1. ∫ 0 1 F t × G ( t )
  2. ∫ 0 1 F t . G ( t )

Passo 1

Precisamos incialmente, calcular:

F t × G t

F t . G ( t )

Começando por F t × G t :

F t × G t = i j k t 1 e t 1 1 1 = 1 i + e t j + t k - 1 k - e t i - t j

F t × G t = 1 - e t i + e t - t j + t - 1 k

Agora F t . G ( t ) :

F t . G t = t , 1 , e t . 1,1 , 1 = t . 1 + 1.1 + e t . 1 = t + 1 + e t

Passo 2

Agora, é só calcular as integrais:

∫ 0 1 F t × G t = ∫ 0 1 1 - e t d t ,   ∫ 0 1 e t - t d t ,   ∫ 0 1 t - 1 d t

∫ 0 1 F t × G t = t - e t 1 0 ,   e t - t 2 2 1 0 , t 2 2 - t 1 0

∫ 0 1 F t × G t = 1 - e 1 - 0 + e 0 , e 1 - 1 1 2 - e 0 + 0 2 2 , 1 2 2 - 1 - 0 2 2 + 0

∫ 0 1 F t × G t = 2 - e 1 ,   e 1 - 3 2 ,   - 1 2

Passo 3

∫ 0 1 F t . G t = ∫ 0 1 t + 1 + e t d t = t 2 2 + t + e t 1 0 = 1 2 2 + 1 + e 1 - 0 2 2 - 0 - e 0

∫ 0 1 F t . G t = 1 2 + e

Resposta

  1. ∫ 0 1 F t × G t = 2 - e 1 ,   e 1 - 3 2 ,   - 1 2
  2. ∫ 0 1 F t . G t = 1 2 + e

Exercício Resolvido #3

George B. Thomas, Cálculo,Volume II,11ª ed. São Paulo: Pearson Education do Brasil Ltda., 2009, pg. 283, exercício 1.

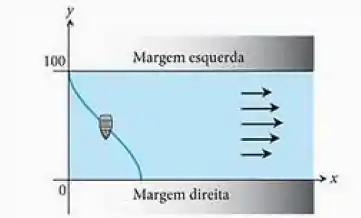
Um rio reto tem 100 m de largura. Um barco a remo deixa a margem no instante t = 0 . A pessoa que está no barco rema a 20 m / m i n sempre na direção da margem direita. A velocidade do rio em ( x , y ) é

v → = - 1 250 y - 50 2 + 10,0 ,   0 < y < 100

  1. Dado que r 0 = ( 0,100 ) , qual é a posição do barco no instante t ?
  2. A que distancia rio abaixo o barco atingirá a margem direita?

Passo 1

Vamos lá: queremos achar a posição do barco em relação a margem e o que temos são informações sobre a velocidade do barco em relação ao rio e a velocidade do rio. Temos então que achar a velocidade do barco em relação a margem para então integrá-la e achar a posição do barco em relação a margem!

A velocidade do barco em relação a margem é igual a soma da velocidade do barco em relação ao rio e da velocidade do rio. Isto é, uma pessoa que está parada na margem do rio vê o barco se movimentando com a sua velocidade em relação as aguas do rio, mas também sendo movimentado pela correnteza do rio.

Nossos dados então são:

v b , r → = 0 , - 20

v r → = - 1 250 y - 50 2 + 10,0

v b , m → = v r + v b , r

Substituindo:

v b , m → = - 1 250 y - 50 2 + 10 , - 20

Passo 2

Opa, mas ai temos que a velocidade do barco em relação a margem está em função de y e sabemos que quando se trata de velocidade, o parâmetro tem que ser o tempo t .

Mas, como só tem gente esperta aqui, a gente sabe que

d y d t = - 20

Porque o barco se aproxima da margem, andando sempre na direção y , no sentindo negativo, com uma velocidade de 20 m / m i n , ou seja, a taxa de variação de da distancia y em relação ao tempo é de - 20 m / m i n .

Então

y = - 20 t + c

Passo 3

Sabemos que y 0 = 100 , ou seja, no instante t = 0 o barco está na posição da margem esquerda.

100 = - 20.0 + c

c = 100

Logo:

y = - 20 t + 100

Passo 4

Pronto, agora já podemos substituir o y na velocidade do barco em relação a margem

v b , m → = - 1 250 y - 50 2 + 10 , - 20

v b , m → = - 1 250 - 20 t + 50 2 + 10 , - 20

v b , m → = - 8 5 t ² + 8 t , - 20

Passo 5

Agora sim podemos integrar a velocidade e recuperar a posição do barco em relação a margem

r t = ∫ v b , m d t  

r t = ∫ - 8 5 t 2 + 8 t , - 20 d t = - 8 15 t 3 + 4 t 2 + c 1 , - 20 t + c 2

Passo 6

Para descobrir ( c 1 , c 2 ) usamos o fato de que r 0 = ( 0,100 ) , assim:

- 8 15 0 3 + 4 0 2 + c 1 = 0

c 1 = 0

- 20 0 + c 2 = 100

c 2 = 100

Logo

r t = - 8 15 t 3 + 4 t 2 , - 20 t + 100

Passo 7

Agora queremos descobrir qual será o valor de x quando y = 0 . Para isso, precisamos descobrir em que valor de t o barco atinge a posição ( x , 0 ) .

Fazemos:

y = - 20 t + 100 = 0

t = 5

Passo 8

Por fim, é só substituir t = 5 no vetor posição para saber qual será o valor da coordenada x :

r t = - 8 15 t 3 + 4 t 2 , - 20 t + 100

r 5 = - 8 15 5 3 + 4 5 2 , - 20.5 + 100

r t = - 200 3 + 100,0

r t = 100 3 , 0

Resposta

a )   r t = - 8 15 t 3 + 4 t 2 , - 20 t + 100

b )   r t = 100 3 , 0

Exercícios de Livros Relacionados

Sejam vec F (t) = t vec i + vec j + e^t vec k e vec G (t) = vec i + vec j + vec k . Calculeint_0^1 vec F (t) * vec G (t) d t
Suponha que F → t é a força resultante que atua, no instante t , sobre uma partícula de massa m que se move no espaço. Mostre que o impulso de F → no intervalo t 1 , t 2 é igual à variação da quantida
Calcule.int_(- 1)^1 [sen 3 t vec i + (1)/(1 + t^2) vec j + vec k] d t
Calcule.int_0^1 [t vec i + e^t vec j] d t
Use a Fórmula 2 para deduzir a Fórmula 7 a partir da Fórmula 8.2.5, no Volume 1, para o caso no qual a curva pode ser representada na forma y = F x ,a ≤ x ≤ b .