Exercícios de Integração de vetores - Lista de Exercícios Resolvida
Questão 2
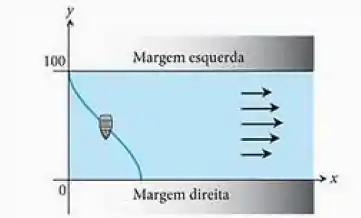
Um rio reto tem de largura. Um barco a remo deixa a margem no instante . A pessoa que está no barco rema a sempre na direção da margem direita. A velocidade do rio em é
- Dado que , qual é a posição do barco no instante ?
- A que distancia rio abaixo o barco atingirá a margem direita?
Questão 4
Seja um campo vetorial irrotacional de classe definido em , onde e . Seja a circunferência de raio 1 centrada em e seja a circunferência de raio centrada em , ambas com sentido anti-horário. Suponha que
- Expresse como uma combinação linear de e com coeficientes racionais, onde é a curva fechada representada no desenho abaixo:
- Supondo que onde
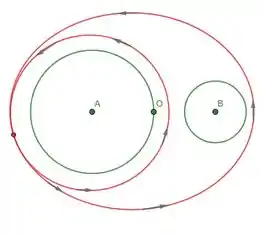
Determine os valores das constantes reais e .
Ver solução completaQuestão 6
Seja um campo vetorial irrotacional de classe definido em , onde e . Seja a circunferência de raio 1 centrada em e seja a circunferência de raio centrada em , ambas com sentido anti-horário. Suponha que
- Expresse como uma combinação linear de e com coeficientes racionais, onde é a curva fechada representada no desenho abaixo:
- Supondo que onde
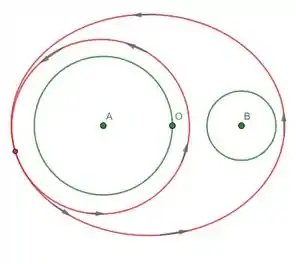
Determine os valores das constantes reais e .
Ver solução completaQuestão 7
Uma partícula se move no plano com vetor posição para cada instante , sendo que no instante ela está na posição . Savendo que o vetor velocidade é dado por
Quanto vale ?
Questão 8
Assinale para verdadeiro e para falso.
- A imagem da função vetorial
- A regra do produto vetorial para derivadas de funções vetoriais nos diz que
- A função vetorial
- Se , então a função vetorial é contínua.
- A curva não é lisa, mas possui reparametrização lisa.
É igual ao conjunto de todos os pontos tais que
Não possui limites laterais em .
Questão 9
Resolva a equação diferencial para como função vetorial de :
Com a condição inicial: .
Ver solução completa